Sur ce thème
Etape 1 : Evaluer les caractéristiques clés
Examinez le centrage et la répartition de la loi de distribution. Evaluez l'impact de l'effectif de l'échantillon sur l'apparence de la boîte à moustaches.
Centrage et répartition
- Médiane
- La médiane est représentée par la ligne dans la boîte. La médiane est une mesure courante du centrage de vos données. La moitié des observations lui sont inférieures ou égales et la moitié des observations lui sont supérieures ou égales.
- Boîte de l'étendue interquartile
- La boîte de l'étendue interquartile représente la moitié centrale (50 %) des données. Elle indique la distance entre les premier et troisième quartiles (Q1-Q3).
- Moustaches
- Les moustaches s'étendent des deux côtés de la boîte. Elles représentent les plages des 25 % inférieurs et des 25 % supérieurs des valeurs de données, à l'exclusion des valeurs aberrantes.
Maintenez le pointeur sur la boîte à moustaches pour afficher une info-bulle indiquant ces statistiques. Par exemple, cette boîte à moustaches des fréquences cardiaques au repos indique que la fréquence cardiaque médiane est de 71. La fréquence cardiaque au repos de la plupart des sujets est située entre 64 et 80, mais la fréquence cardiaque de certains sujets peut baisser jusqu'à 48 ou atteindre 100.
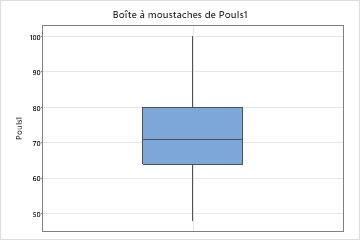
Examinez toute caractéristique surprenante ou indésirable dans la boîte à moustaches. Par exemple, une boîte à moustaches peut indiquer que la longueur médiane de planches en bois est bien inférieure à la longueur cible qui est de 8 pieds.
Remarque
Etant donné que les quartiles de la boîte à moustaches sont des valeurs calculées, il se peut qu'ils ne correspondent pas à des observations réelles dans votre fichier de données. Pour plus d'informations sur la procédure d'interprétation des quartiles, reportez-vous à la rubrique Que sont les quartiles ?. Pour des informations précises sur la façon dont les quartiles sont calculés, reportez-vous à la rubrique Méthodes et formules pour le récapitulatif graphique.
Effectif d'échantillon (n)
L'effectif de l'échantillon peut avoir une incidence sur l'apparence du graphique.
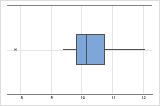
n = 15
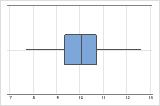
n = 500
La boîte à moustaches est plus adaptée lorsque l'effectif d'échantillon est d'au moins 20. Si l'effectif d'échantillon est trop petit, les quartiles et les valeurs aberrantes apparaissant dans la boîte à moustaches risquent de ne pas être significatifs. Si l'effectif d'échantillon est inférieur à 20, envisagez plutôt d'utiliser un diagramme des valeurs individuelles.
Etape 2 : Rechercher des indicateurs de données non normales ou aberrantes
Les données asymétriques peuvent indiquer la présence de données non normales. Les valeurs aberrantes peuvent indiquer la présence d'autres conditions dans vos données.
Données asymétriques
Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. L'asymétrie indique que les données peuvent ne pas être normalement distribuées.
Ces boîtes à moustaches illustrent des données asymétriques. La boîte à moustaches avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. La boîte à moustaches avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
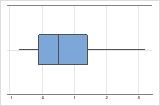
Asymétrie à droite
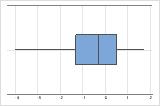
Asymétrie à gauche
Si vous savez que vos données ne sont pas naturellement asymétriques, étudiez-en les causes possibles. Pour analyser les données très asymétriques, consultez la rubrique sur les observations relatives aux données pour l'analyse afin de vous assurer que vous pouvez utiliser des données non normales.
Valeurs aberrantes
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur vos résultats. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
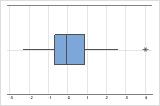
Conseil
Maintenez le pointeur sur la valeur aberrante pour identifier le point de donnée.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
Étape 3 : Évaluer et comparer des groupes
Si votre boîte à moustaches comporte des groupes, évaluez et comparez le centrage et la dispersion des groupes.
Centres
Recherchez des différences entre les centres des groupes.
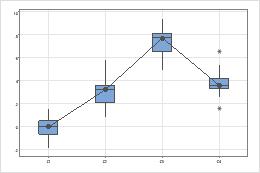
Dispersions
Recherchez les différences entre les dispersions des groupes.
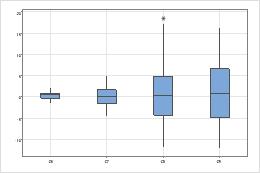
- Utilisez un test à 2 variances si vous n'avez que deux groupes.
- Utilisez un test de l'égalité des variances si vous avez trois groupes ou plus.
