Methods and formulas for fits and residuals in Fit Regression Model and Linear Regression

Select the method or formula of your choice.

In This Topic

Fit
Standard error of fitted value (SE Fit)
Confidence interval for a fitted value (CI)
Residuals
Standardized residual (Std Resid)
Standardized residual (Std Resid) with validation
Deleted (Studentized) residuals

Fit

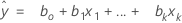
Notation

Term	Description
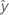	fitted value
x_k	k^th term. Each term can be a single predictor, a polynomial term, or an interaction term.
b_k	estimate of k^th regression coefficient

Standard error of fitted value (SE Fit)

The standard error of the fitted value in a regression model with one predictor is:

The standard error of the fitted value in a regression model with more than one predictor is:

For weighted regression, include the weight matrix in the equation:

When the data have a test data set or K-fold cross validation, the formulas are the same. The value of s² is from the training data. The design matrix and the weight matrix are also from the training data.

Notation

Term	Description
s²	mean square error
n	number of observations
x₀	new value of the predictor
	mean of the predictor
x_i	i^th predictor value
x₀	vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term
x'₀	transpose of the new vector of predictor values
X	design matrix
W	weight matrix

Confidence interval for a fitted value (CI)

Formula

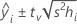
For regression, the following formula gives the confidence bounds for a fitted value:

For weighted regression, the formula includes the weights:

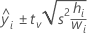
where t_v is the 1–α/2 quantile of the t distribution with v degrees of freedom for a two-sided interval. For a 1-sided bound, t_v is the 1–α quantile of the t distribution with v degrees of freedom.

When you use a test data set or k-fold cross-validation, the degrees of freedom and the mean square error are from the training data set.

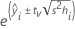
When you use a Box-Cox transformation, apply the inverse transformation to the confidence interval formula to find the bounds in the units of the original response. For example, if the Box-Cox transformation is the natural log, then the following formula gives the inverse transformation:

Notation

Term	Description
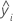	fitted value
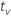	quantile from the t distribution
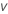	degrees of freedom
	mean square error
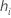	leverage for the i^th observation
w_i	weight for the i^th observation

Residuals

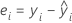
The residual is the difference between an observed value and the corresponding fitted value. This part of the observation is not explained by the model. The residual of an observation is:

Notation

Term	Description
y_i	i^th observed response value
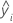	i^th fitted value for the response

Standardized residual (Std Resid)

Standardized residuals are also called "internally Studentized residuals."

Formula

Notation

Term	Description
e_i	i ^th residual
h_i	i ^th diagonal element of X(X'X)^–1X'
s²	mean square error
X	design matrix
X'	transpose of the design matrix

Standardized residual (Std Resid) with validation

For validation data, the denominator of the formula for the standardized residual adds the leverage instead of subtracting the leverage.

Formula

For weighted regression, the formula includes the weight:

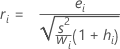
Notation

Term	Description
e_i	i ^th residual in the validation data set
h_i	leverage for the i^th validation row
s²	mean square error for the training data set
w_i	weight for the i^th observation in the validation data set

Deleted (Studentized) residuals

Also called the externally Studentized residuals. The formula is:

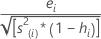
Another presentation of this formula is:

The model that estimates the i^th observation omits the i^th observation from the data set. Therefore, the i^th observation cannot influence the estimate. Each deleted residual has a student's t-distribution with 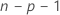degrees of freedom.

Notation

Term	Description
e_i	i^th residual
s_(i)²	mean square error calculated without the i^th observation
h_i	i ^th diagonal element of X(X'X)^–1X'
n	number of observations
p	number of terms, including the constant
SSE	sum of squares for error