There are different calculations for the gap pools depending on whether you have specified shift or drift (variation expansion) factors for the elements and which gap specifications are given.
Mean shift factor only
- No gap specification
-
μPool = σGap,LT[Zp – Z.BenchGap,LT]
σ2Pool = 0
- Lower gap specification only
-
μPool = σGap,LT[Zp – Z.BenchGap,LT]
σ2Pool = 0
- Upper gap specification only
-
μPool = σGap,LT[Z.BenchGap,LT – Zp]
σ2Pool = 0
- Both gap specifications
-
μPool = 0
σ2Pool = σ2adj,LT – σ2Gap,LT*
* where if  , then
, then 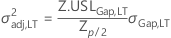
or else σ2adj,LT is the unique solution to:

Variation expansion factor only, or both mean shift factor and variation expansion factor
- One or no gap specification
-
μPool = 0

- Both gap specifications
-
μPool = 0
σ2Pool = σ2adj,LT – σ2Gap,LT *
Note
σ2Pool = 0 if T=LSL or T=USL and Zp=0
* where if  , then
, then 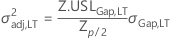
or else σ2adj,LT is the unique solution to:

Notation
| Term | Description |
|---|---|
| Ci | Diametrical correction of the ith element |
| Di | Drift factor for the ith element |
| Ni | Complexity of the ith element |
| Si | Shift factor for the ith element |
| σi | Standard deviation of the ith element |
| σadj,i | Adjusted standard deviation of the ith element |
| T | Gap targeted value (if not available, T = μGap,ST) |
| Ti | Nominal value of the ith element |
| μi | Mean of the ith element |
| μadj,i | Adjusted mean of the ith element |
| Vi | Directional vector of the ith element |
| wi | Allocation weight for the mean pool or the variance pool, ith element |
| Z.BenchGap,LT | Benchmark Z (long-term) of the gap |
| Z.BenchGap,ST | Benchmark Z (short-term) of the gap |
| Z.Benchi,LT | Benchmark Z (long-term) of the ith element |
| Z.Benchi,ST | Benchmark Z (short-term) of the ith element |
| ZP | Z-value, which gives desired PPM (right tail) for long-term gap distribution |
