In This Topic
Coefficient (Coef)
Minitab uses least squares estimation to calculate the coefficients.
In matrix terms, the least squares estimates of the coefficients are:
b = (X'X)-1X'y
For more information on coefficients of higher order models, see Cornell1.
Notation
| Term | Description |
|---|---|
| X | design matrix |
| y | response column |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
Standard error of the coefficient (SE Coef)
For simple linear regression, the standard error of the coefficient is:
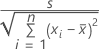
The standard errors of the coefficients for multiple regression are the square roots of the diagonal elements of this matrix:
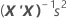
Notation
| Term | Description |
|---|---|
| xi | ith predictor value |
 | mean of the predictor |
| X | design matrix |
| X' | transpose of the design matrix |
| s2 | mean square error |
T-value
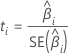
Notation
| Term | Description |
|---|---|
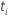 | test statistic for the 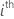 coefficient coefficient |
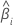 | 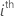 estimated coefficient estimated coefficient |
 | standard error of the 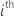 estimated coefficient estimated coefficient |
P-value – Coefficients table
The two-sided p-value for the null hypothesis that a regression coefficient equals 0 is:
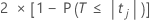
The degrees of freedom are the degrees of freedom for error, as follows:
n – p
Notation
| Term | Description |
|---|---|
 | The cumulative distribution function of the t distribution with degrees of freedom equal to the degrees of freedom for error. |
| tj | The t statistic for the jth coefficient. |
| n | The number of observations in the data set. |
| p | The sum of the degrees of freedom for the terms. |
Variance inflation factor (VIF)
The VIF can be obtained by regressing each predictor on the remaining predictors and noting the R2value.
Formula
For predictor xj, the VIF is:

Notation
| Term | Description |
|---|---|
| R2( xj) | coefficient of determination with xj as the response variable and the other terms in the model as the predictors |
