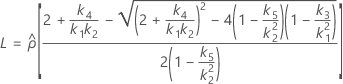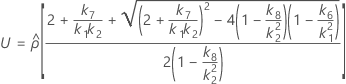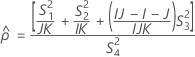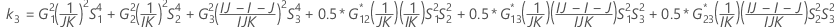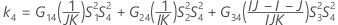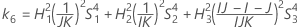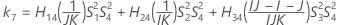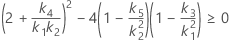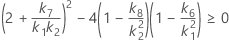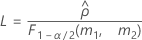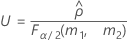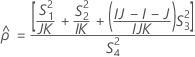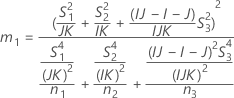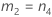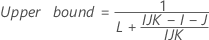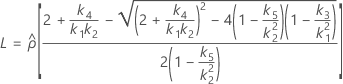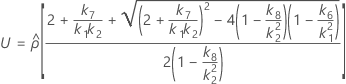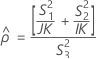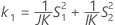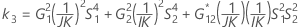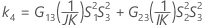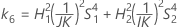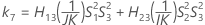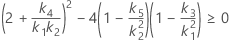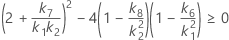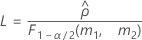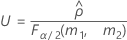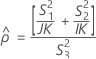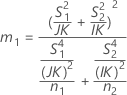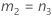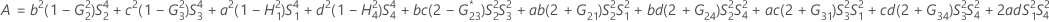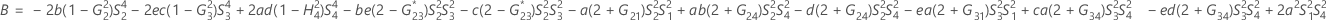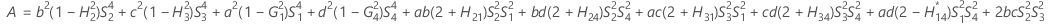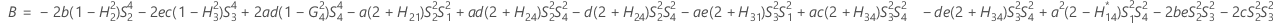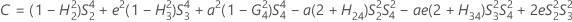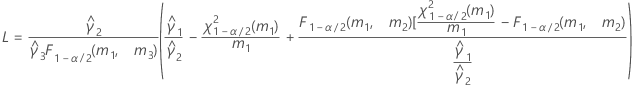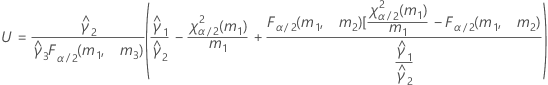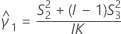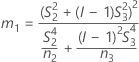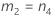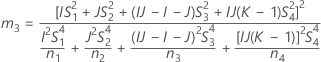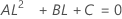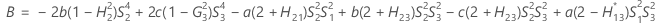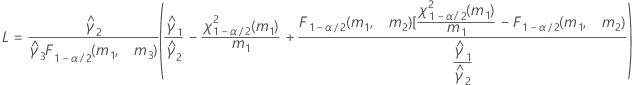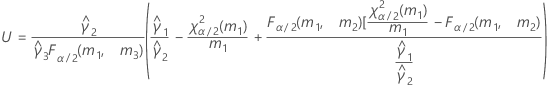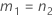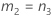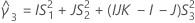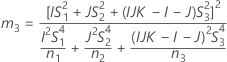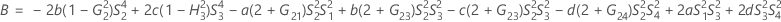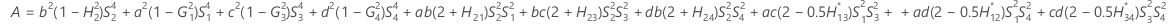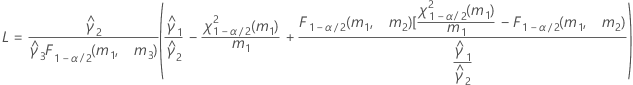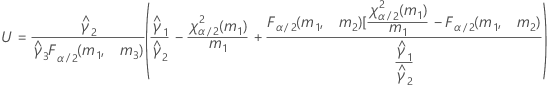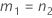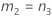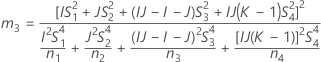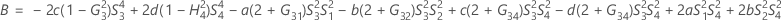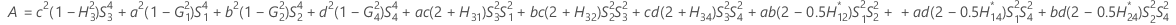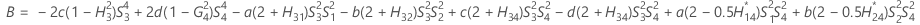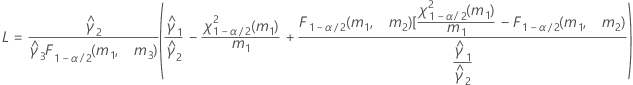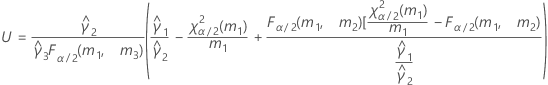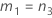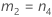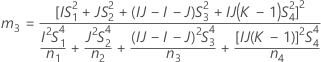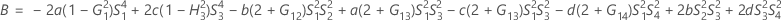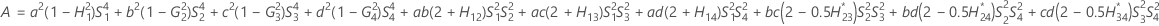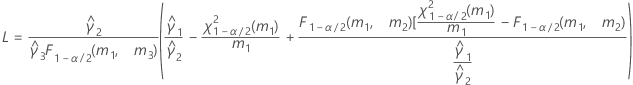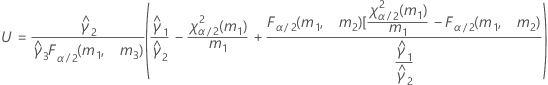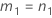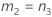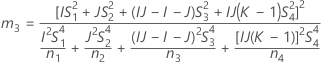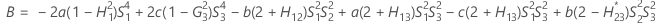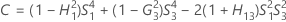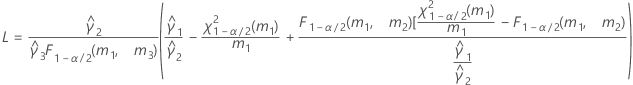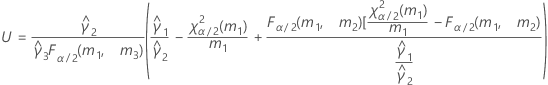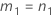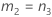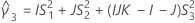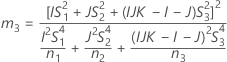In This Topic
- Confidence interval for the ratio of the repeatability variance and the total variance
- Confidence interval for the ratio of the reproducibility variance and the total variance
- Confidence interval for the ratio of the operator variance and the total variance
- Confidence interval for the ratio of the interaction variance and the total variance
- Confidence interval for the ratio of the part variance and the total variance
- Confidence interval for the ratio of the gage variance and the total variance
Confidence interval for the ratio of the repeatability variance and the total variance
With operator
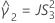
When the operator and interaction term are included, there are two possible calculation methods. Minitab first calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses the Satterthwaite approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
-

- Satterthwaite approximation
- The formulas for the lower and upper bounds still hold, except L and U are defined as follows:
Without operator term
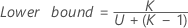

Without interaction term
When the operator and interaction term are included, there are two possible calculation methods. Minitab first calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses the Satterthwaite approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
-
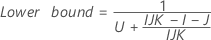
- Satterthwaite approximation
- The formulas for the lower and upper bounds still hold except L and U are defined as follows:
Notation
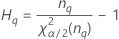
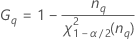
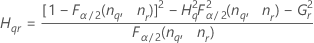
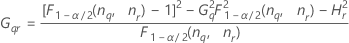
| Term | Description |
|---|---|
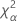 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
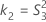
Confidence interval for the ratio of the reproducibility variance and the total variance
With interaction tern
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
- The lower and upper bounds for an approximate (1- α) * 100% confidence interval are calculated by solving quadratic equations.
- Second method
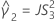
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated as follows:
Without interaction term
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated by solving quadratic equations. Lower bound, L, equals J times the smaller solution to the following equation.
- Second method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated as follows:
Notation
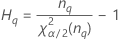
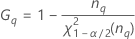
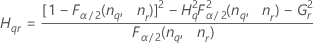
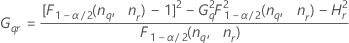
| Term | Description |
|---|---|
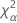 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
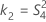
| a | I |
| b | J |
| c | (IJ – I –J) |
| d | IJ(K-1) |
| e | I – 1 |
Confidence interval for the ratio of the operator variance and the total variance
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated by solving quadratic equations.
- Second method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated as follows:
Notation
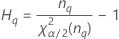
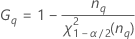
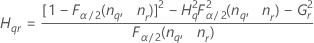
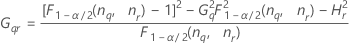
| Term | Description |
|---|---|
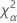 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Confidence interval for the ratio of the interaction variance and the total variance
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated by solving quadratic equations.
- Second method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated as follows:
Notation
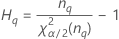
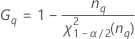
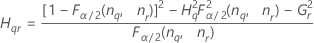
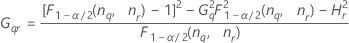
| Term | Description |
|---|---|
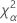 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Confidence interval for the ratio of the part variance and the total variance
With operator and interaction term
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
- MLS method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated by solving quadratic equations.
- Second method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated as follows:
Without operator term
Lower bound = 1 – (the lower bound for the ratio of the repeatability variance and the total variance)
Upper bound = 1 – (the upper bound for the ratio of the repeatability variance and the total variance)
Without interaction term
- MLS method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated by solving quadratic equations.
- Second method
- The lower and upper bounds for an approximate (1 – α) * 100% confidence interval are calculated as follows:
Notation
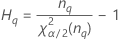
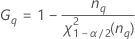
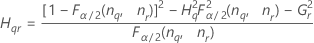
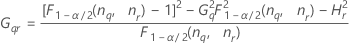
| Term | Description |
|---|---|
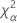 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Confidence interval for the ratio of the gage variance and the total variance
Lower bound = 1 – (lower bound of the CI for the ratio of the part variance and the total variance)
Upper bound = 1 – (upper bound of the CI for the ratio of the part variance and the total variance)