Descargar la macro
Asegúrese de que Minitab sepa dónde buscar la macro descargada. Elija . En Ubicación de la macro, vaya a la ubicación donde guarda los archivos de macro.
Important
Si utiliza un explorador web más antiguo, cuando haga clic en el botón Descargar, el archivo podría abrirse en Quicktime, que comparte la extensión de archivos .mac con las macros de Minitab. Para guardar la macro, haga clic con el botón derecho en el botón Descargar y elija Guardar destino como.
Entradas requeridas
Necesita una columna de datos de series de tiempo.
Entradas opcionales
- AR K…K
- Si tiene parámetros autorregresivos estimados y desea ejecutar la verificación del modelo espectral, ingrese estos parámetros aquí.
- DIF K
- Si tiene un componente de diferenciación, ingrese el orden de la diferenciación aquí.
- MA K…K
- Si tiene parámetros de promedio móvil estimados y desea ejecutar la verificación del modelo espectral, ingrese estos parámetros aquí.
- VARIANCE K
- Ingrese su varianza estimada (predeterminada = 1.0).
- SMOOTH K
- Ingrese la longitud del promedio móvil (predeterminado = 3). La longitud del promedio móvil debe ser un valor entero impar.
- ONEDOC
- Ingrese esto si desea que todas las gráficas estén en una misma página.
- SPERIOD C C
- Ingrese esto si desea almacenar las coordenadas del periodograma. La primera columna contendrá I(omega) y la segunda contendrá omega.
- SCUMUL C C C C
- Ingrese esto si desea almacenar las coordenadas del periodograma acumulado. La primera columna contendrá U(j), la segunda columna contendrá el límite de significancia superior, la tercera columna contendrá el límite de significancia inferior y la cuarta columna contendrá el eje X.
- SSPEC C C C C
- Ingrese esto si desea almacenar las coordenadas de la estimación espectral. La primera columna contendrá la estimación espectral, la segunda columna contendrá el límite de confianza superior, la tercera columna contendrá el límite de confianza inferior y la cuarta columna contendrá omega.
- SMODEL C C C C
- Ingrese esto si desea almacenar las coordenadas de la verificación del modelo espectral. La primera columna contendrá F(omega), la segunda columna contendrá el límite de confianza superior, la tercera columna contendrá el límite de confianza inferior, la cuarta columna contendrá las estimaciones espectrales y la quinta columna contendrá omega.
Ejecución de la macro
Supongamos que los datos están en C1. Para ejecutar la macro, elija y escriba:
%SPECTRAL C1Haga clic en Corrida.
Información adicional
Periodograma
El periodograma es una herramienta que se puede utilizar para detectar componentes cíclicos en una serie de tiempo. El periodograma se define de la siguiente manera:
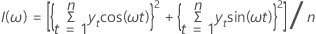
Si bien el periodograma se define para ω = 0, este punto se excluye debido a que corresponde a la media de la muestra (que no es de interés). Si n es impar, excluimos ω =π.
Periodograma acumulado
El periodograma acumulado es una aplicación directa del periodograma para probar la hipótesis de que una serie de tiempo particular es una secuencia de ruido blanco. El periodograma acumulado es una efectiva herramienta de diagnóstico para los residuos. El periodograma acumulado se define como:
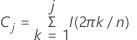
j=1,...,m donde m es el entero más grande estrictamente menor que n/2
Una gráfica de U j en función de j /(m −1) se conoce como el periodograma acumulado.
También podemos definir valores críticos para probar la hipótesis de ruido blanco. El nivel de significancia que utiliza la macro es 10 % (valor crítico = 1.224). Las dos líneas paralelas con la siguiente Y-intersección definen la región crítica:
Estimación espectral
La estimación espectral,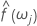 
, se puede derivar simplemente tomando un promedio móvil de orden 2p+1 (donde p es un valor entero positivo) de las ordenadas calculadas por el periodograma. También podemos establecer límites a esta estimación espectral:
Los límites de confianza superior e inferior se pueden definir como:
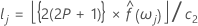
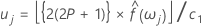
Espectro de un proceso ARMA
La estimación espectral es la estimación del espectro con base en los datos. El espectro se basa en los valores reales de la población de los parámetros del modelo. El espectro de un proceso AR(p) se puede definir de la manera siguiente:
El espectro de un proceso MA(q) se puede definir de la manera siguiente:
El espectro de un proceso ARMA (p, q) (donde p y q son ordenes) se puede definir de la manera siguiente:
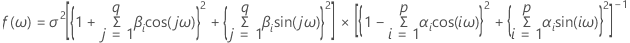
Verificación del modelo espectral para un proceso ARIMA
Podemos comparar la estimación espectral calculada a partir de una serie de tiempo observada con el espectro real basándonos en los parámetros del modelo. Por intuición, si la estimación espectral es, con proximidad, estadísticamente igual al espectro real, podemos concluir que nuestros parámetros del modelo estimados son adecuados para modelar la serie.
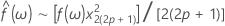
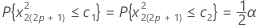
Por lo tanto, podemos establecer límites de confianza para determinar si la estimación espectral se encuentra o no dentro de estos límites.
Example 1
Para un ejemplo de periodograma, periodograma acumulado y estimación espectral, considere el conjunto de datos 'Ciclo 1, Fase folicular tardía (Diggle, p. 228). Para ejecutar la macro, elija y escriba:
%SPECTRAL C1En primer lugar, el periodograma (no mostrado) indica que esta serie tiene un componente cíclico debido a su pico predominante. Algunas veces, el eje X se transforma en una escala más significativa de manera que pueda determinarse más fácilmente en cuál punto en el tiempo está ocurriendo el componente cíclico. Por esta razón, la macro tiene opciones de almacenamiento de manera que el usuario pueda transformar el eje (entonces puede utilizar las capacidades gráficas de Minitab para generar gráficas). En segundo lugar, el periodograma acumulativo indica que esta serie no es una secuencia de ruido blanco porque algunos de los puntos de datos van más allá de los límites de significancia (representados por las líneas punteadas paralelas). Finalmente, la estimación espectral (calculada mediante el promedio móvil de 3 puntos predeterminado) se muestra con la línea roja mientras los límites de confianza se muestran con líneas punteadas. Esta gráfica nos da una idea acerca de cómo puede lucir el espectro real de población. Todas las tres gráficas coinciden con las gráficas mostradas en Diggle (p. 52, 55, 106).
Ejemplo 2
Para una análisis completo de ARIMA, considere el conjunto de datos 'Ciclo 1, Fase folicular temprana (Diggle, p. 228). Primero, calcule el periodograma, el periodograma acumulativo y la estimación espectral. También colocaré estas tres gráficas en una página utilizando el subcomando 'Onedoc'. Elija y escriba:
%SPECTRAL C2;
ONEDOC.
Las gráficas (no se muestran) evidencian que esta serie de tiempo no es una secuencia de ruido blanco, porque tanto el periodograma como la estimación espectral indican una serie de baja frecuencia debido a los picos predominantes con valores de omega pequeños, y el periodograma acumulado muestra puntos significativos. Por lo tanto, utilizaremos MINITAB para modelar esta serie de tiempo usando el algoritmo de ARIMA. Luego de considerar diferentes modelos, el mejor es un AR(1).
Ahora, utilizaremos la macro para evaluar este modelo empírico. Note cómo la estimación del parámetro autorregresivo y la estimación de la varianza (a partir de la salida de ARIMA) se ingresan en el lenguaje de comandos siguiente. Elija y escriba:
%SPECTRAL C2;
AR 0.586;
VARIANCE 0.20603;
ONEDOC.
Las gráficas resultantes solo muestran una vez más las gráficas ya observadas junto con la verificación del modelo espectral. En referencia a la verificación del modelo espectral, los círculos rojos representan la estimación espectral y la línea continua es el espectro "real" con base en nuestros parámetros estimados del modelo ARIMA. Las líneas punteadas representan los límites de confianza del espectro "real". Debido a que casi todos los promedios móviles de tres puntos (los círculos rojos) se encuentran dentro del intervalo de confianza del espectro real, podemos concluir que el modelo es válido. Por último, sería recomendable ejecutar la macro en los residuos con el fin de asegurar que sean residuos de ruido blanco. El periodograma acumulado efectivamente indica que los residuos describen una secuencia de ruido blanco.
Referencias
Diggle, P. J. Time Series, A Biostatistical Introduction. Oxford: Clarendon Press, 1990.
