Descargar la macro
Asegúrese de que Minitab sepa dónde buscar la macro descargada. Elija . En Ubicación de la macro, vaya a la ubicación donde guarda los archivos de macro.
Important
Si utiliza un explorador web más antiguo, cuando haga clic en el botón Descargar, el archivo podría abrirse en Quicktime, que comparte la extensión de archivos .mac con las macros de Minitab. Para guardar la macro, haga clic con el botón derecho en el botón Descargar y elija Guardar destino como.
Entradas requeridas
Necesita hasta cinco matrices de diseño.
Entradas opcionales
- MODEL tipo de modelo
- Especifica el modelo que se probará cuando se ejecute el experimento. El valor predeterminado es "interacción". Puede ingresar múltiples modelos, tales como lineal, cuadrático, interacción, cuadrático puro. Cada modelo incluye los términos siguientes:
- Lineal: términos lineales y constantes
- Interacción: términos constantes, lineales y de productos cruzados
- Cuadrático: interacciones más términos al cuadrado
- Cuadrático puro: términos constantes, lineales y al cuadrado
- RESOLUTION K
- Utilícese para especificar el número de los puntos de diseño muestreados que se utilizaron para estimar el mínimo, máximo y la varianza de predicción integrada en cada valor diferente del radio. Para diseños rotables, se puede seleccionar una resolución baja. Para diseños no rotables, se puede aumentar la resolución a medida que aumenta el número de factores. La predeterminada es de 500 puntos de diseño.
- INCREMENT K
- Utilícese para especificar el incremento del radio. Se puede cambiar este valor para mostrar la gráfica con una resolución más alta o más baja. El valor predeterminado es 0.1 unidades codificadas.
- MAXDIST K
- Indica la distancia máxima del radio. Por opción predeterminada, esta se define como la distancia más larga al punto de diseño que está más distante del centro del diseño. Para una VDG que se basa en diseños múltiples, la MAXDIST se establece como la distancia más larga desde todos los diseños.
Ejecución de la macro
Supongamos que los factores de un CCD se han copiado en una matriz M1 y que los factores de un diseño de Box-Behnken se han almacenado en M2. Para ejecutar la macro, elija y escriba:
%VDG M1 M2;
MODEL "cuadrático";
RESOLUTION 150.Haga clic en Corrida.
Más información
Gráficas de dispersión de la varianza y diseño de experimentos
Las gráficas de dispersión de la varianza son herramientas gráficas utilizadas en el proceso de selección de un diseño de experimento (DOE). Estas gráficas muestran la varianza de la predicción escalada de un DOE a través del espacio de diseño y generalmente se utilizan para comparar diseños de superficie de respuesta. Sin embargo, las gráficas de dispersión de la varianza también pueden utilizarse para comparar el desempeño de múltiples diseños para un modelo específico, tal como un modelo lineal, un modelo lineal con términos de interacción, un modelo lineal con términos cuadráticos o un modelo totalmente cuadrático.
Historia y antecedentes de VDG
La VDG fue desarrollada originalmente por Giovannitti-Jensen y Myers (1989) y Myers et al. (1992) para mostrar una instantánea de la estabilidad de la varianza de la predicción escalada a través del espacio de diseño.
Matemáticamente, la varianza de la predicción escalada puede estimarse con la siguiente ecuación:
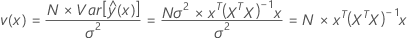
donde v(x) es la varianza de la predicción escalada en el punto X y, como se muestra arriba, no depende de los datos de respuesta, solamente de la matriz de diseño X. En otras palabras, la varianza de la predicción escalada depende del número de corridas del experimento, la matriz de covarianza y el punto en el cual usted está evaluando la varianza de la predicción. Debido a que la varianza de la predicción escalada que muestra la VDG es independiente de los datos de respuesta, la VDG permite evaluar la bondad de un diseño a priori.
En general, una VDG se construye con cuatro componentes básicos:
- Una gráfica de la varianza esférica en función del radio r. La varianza esférica es v(x) promediado (integrado) sobre la superficie de una esfera de radio r.
- · Una gráfica de la máxima varianza de la predicción en un radio r para valores múltiples de r empezando desde el origen (r comienza en cero y luego va incrementando poco a poco hasta llegar al punto de diseño que está más distante del origen).
- · Una gráfica de la mínima varianza de la predicción en un radio r para valores múltiples de r empezando desde el origen.
- · Una línea horizontal en v(x) = p, donde p es el número de parámetros en el modelo que se va a ajustar. En un diseño "óptimo", la máxima varianza de la predicción sería menor que o igual a p para todos los puntos en el espacio de diseño.
La VDG muestra las varianzas promedio, máxima y mínima de la predicción escalada en diferentes valores de r, que representa la distancia desde cualquier punto dado hasta el origen o el centro del diseño.
Uso de una VDG para evaluar otros aspectos de un diseño
Utilizando una VDG, usted puede evaluar el desempeño de un diseño individual en términos de su varianza de predicción. También puede utilizar la VDG para comparar dos o más diseños. Otro uso de una VDG es para evaluar el efecto de agregar puntos centrales a un diseño.
Una VDG también puede utilizarse para determinar si un diseño es rotable. En un diseño rotable, las tres líneas (mínima, promedio y máxima) de la gráfica coincidirán. Si las líneas mínima, promedio y máxima no coinciden, el diseño 3^k no es rotable.
Simulación Monte Carlo para estimar la varianza de la predicción
Esta sección avanzada describe los métodos matemáticos utilizados para estimar las varianzas de predicción mínima, máxima y promedio mostradas en una VDG. Si solo está interesado en cómo ejecutar una macro para mostrar e interpretar una VDG, puede omitir esta sección.
Como ya se indicó, para un valor fijo del radio, se debe realizar una búsqueda para encontrar la varianza de la predicción escalada mínima, máxima e integrada. El método seleccionado para la macro de Minitab se basa en la simulación Monte Carlo y en la capacidad para buscar de manera uniforme a puntos equidistantes del centro x = (0,0,…,0)T del diseño.
Se deben calcular tres cantidades a diferentes distancias desde el origen: 1) la mínima varianza de predicción, 2) la máxima varianza de predicción, y 3) la varianza de predicción integrada. Hay múltiples formas de encontrar estas cantidades. Un método es mediante el uso de un algoritmo de programación no lineal para encontrar la varianza de predicción mínima y máxima. Sin embargo, el método que elegimos para estimar estas cantidades es tomar una muestra uniforme y buscar un conjunto grande de puntos diferentes que estén a la misma distancia del centro del diseño para diferentes valores de r. A partir del espacio de puntos equidistantes, se puede garantizar el cálculo apropiado de las varianzas de predicción mínima y máxima teniendo dos condiciones satisfechas: Primero, el muestreo de puntos equidistantes debe ser uniforme. En otras palabras, no puede haber regiones donde los puntos equidistantes tengan más probabilidades que otros de ser elegidos. La segunda, el número de puntos tiene que se lo suficientemente grande como para cubrir todo el espacio de posibles puntos de diseño.
Dado que todos los puntos que se tienen que muestrear están equidistantes, el problema del muestreo es equivalente a encontrar una forma adecuada de obtener puntos desde una bola n o hiperesfera para un radio determinado.
El procedimiento está descrito en Marsaglia (1972) y se resume a continuación:
- Genere un vector n-dimensional de variables aleatorias normales (por ejemplo, de una distribución normal estándar). Sea este vector x = (x1, x2,…,xn). Cree múltiple vectores x.
- Calcule el radio ρ para todos los puntos x que haya generado.

- Transforme cada uno de los puntos de diseño originales obtenidos en el paso 1 multiplicando cada entrada del vector x por r, donde r representa el radio de la hiperesfera a partir de la cual está realizando el muestreo.
Hemos ilustrado cómo realizar el muestreo de puntos en una hiperesfera de radio r constante. Podemos utilizar esta técnica de muestreo para estimar la varianza máxima o mínima de la predicción. Utilizando estas muestras, con base en la ley débil de los grandes números, la varianza promedio de la predicción de los puntos de diseño muestreados se puede utilizar para estimar la varianza de predicción integrada real siempre y cuando n sea grande.
Referencias
[1] Marsaglia G. "Choosing a Point from the Surface of a Sphere". The Annals of Mathematical Statistics, Vol. 43, No. 2 (1972), pp. 645-646.
[2] Myers R, Montgomery D. (2002). (2002). Response Surface Methodology - Process and Product Optimization Using Designed Experiments, Second Edition. John Wiley & Sons, Inc.
