Descargar la macro
Asegúrese de que Minitab sepa dónde buscar la macro descargada. Elija . En Ubicación de la macro, vaya a la ubicación donde guarda los archivos de macro.
Important
Si utiliza un explorador web más antiguo, cuando haga clic en el botón Descargar, el archivo podría abrirse en Quicktime, que comparte la extensión de archivos .mac con las macros de Minitab. Para guardar la macro, haga clic con el botón derecho en el botón Descargar y elija Guardar destino como.
Entradas requeridas
- Una columna de datos de respuesta numéricos
- Una columna correspondiente de niveles de factores
Nota
Usted puede utilizar datos no apilados especificando el subcomando UNSTACKED.
Entradas opcionales
- UNSTACKED
- Especifique si los datos no están apilados.
- FALPHA
- Utilícese para especificar el nivel de significancia por familia deseado (el predeterminado es 0.20).
- CONTROL C
- Utilícese para especificar que la columna (C) sea el control.
Nota
Si los datos están apilados, la respuesta del grupo de control no debe estar en la misma columna que la respuesta de los demás niveles de los factores. La respuesta del grupo de control debe estar en una columna individual.
Ejecución de la macro
Supongamos que los datos de respuesta se encuentran en C1 y los niveles de los factores en C2. Para ejecutar la macro, elija y escriba lo siguiente:
%KRUSMC C1 C2Haga clic en Corrida.
Salida
La primera parte de la salida mostrará el número de comparaciones (k) realizadas,
 , el nivel de significancia por familia (α), el nivel de significancia individual de Bonferroni (β),
, el nivel de significancia por familia (α), el nivel de significancia individual de Bonferroni (β),  y el valor Z crítico bilateral.
y el valor Z crítico bilateral.
La siguiente sección muestra las diferencias de los rangos de las medias grupales estandarizadas (θ) y los valores p asociados con estas diferencias. Note que estas tablas son simétricas, de modo que hay asteriscos en la parte triangular superior de la tabla. Además, hay ceros a lo largo de la diagonal de la tabla debido a que la diagonal representa una comparación entre un grupo y sí mismo (estas comparaciones son insignificantes y no se consideran en el análisis). Un ejemplo de cómo leer esta tabla es el siguiente: ¿cuál es la diferencia entre los grupos 2 y 4? La tercera sección muestra los intervalos de confianza del signo para las medianas. Los niveles de confianza para estos intervalos se controlan usando su nivel de significancia por familia. Como estos intervalos se controlan en un nivel de significancia por familia general, podemos comparar estos intervalos en parejas (Apéndice 2). Es importante recordar que la confianza deseada pudiera no alcanzarse para todos o algunos intervalos. Además, esta cobertura "general" del nivel de significancia por familia no es exacta cuando los tamaños de las muestras son diferentes, pero suele ser una aproximación razonable.
La sección final nos muestra cuáles son nuestras diferencias "significativas" (si las hubiera). En esta sección, presento el valor z, el valor z crítico y el valor p asociado con el valor z.
La gráfica muestra las diferencias estandarizadas de los rangos de las medias grupales no absolutas. Este gráfica también es muy útil porque podemos examinar no solo la magnitud de las diferencias de los grupos sino también la dirección. Además, muestra los valores z críticos positivos y negativos para que se puede ver si una diferencia es "significativa".
Empates en los datos
Si hay empates en los datos, se calcula una constante de eliminación de sesgo (o factor de corrección) de 2. Luego se ajusta el estadístico H 3. La desviación estándar (ξ) también se ajusta por este factor de corrección 4. La salida dará tablas tanto ajustadas como no ajustadas. Sin embargo, solamente daré valores p para las tablas ajustadas porque estas son las tablas que se deben utilizar. La principal razón para mostrar las tablas no ajustadas es para mostrar los efectos que tienen los empates en los valores z. Si los empates son extremadamente extensos, se debe cuestionar la validez de los datos porque estas pruebas asumen que las distribuciones son continuas. Con frecuencia, los empates tendrán poco o ningún impacto en sus conclusiones.
Reconocimientos
Gracias al Dr. Tom Hettmansperger (de la Universidad del Estado de Pennsylvania) por su revisión de esta macro, nuestras numerosas discusiones sobre este trabajo y por su tiempo y paciencia en general. Gracias también al Sr. Nicholas Bolgiano y al Sr. Mike Delozier (Minitab, Inc.) por sus sugerencias y críticas relacionadas con la macro.
Información adicional
Prueba de Dunn
Una manera efectiva de realizar inferencias simultáneas en parejas fue presentada por Dunn (1964). Primero combinamos los datos, los jerarquizamos, hallamos los rangos de las medias grupales y luego obtenemos las diferencias absolutas estandarizadas de estos rangos promedio.
Supongamos que k = el número de tratamientos, 
Sea 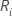 = la suma de los rangos para el i-ésimo tratamiento, i = 1,…,k
= la suma de los rangos para el i-ésimo tratamiento, i = 1,…,k
Sea 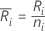
Donde 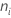 = el número de observaciones del i-ésimo tratamiento
= el número de observaciones del i-ésimo tratamiento
Sea 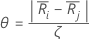
Donde j=l,...,k y j  i
i
Donde 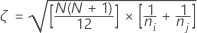
Estadístico H
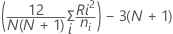
Donde 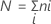
Entonces declararemos "significancia" si:

Donde 
Donde α es un valor de nivel de significancia por familia especificado, 
