Un ingeniero de calidad de una fábrica de motores quiere realizar una prueba de bimodalidad en pistones de dos proveedores. El ingeniero mide las longitudes de una muestra aleatoria de 100 pistones de cada uno de los proveedores.
El script usa el paquete diptest para R para probar si los datos son unimodales. Si la prueba rechaza la hipótesis nula para datos unimodales, entonces el script asume que los datos son una mezcla de dos distribuciones normales. El script utiliza el paquete mixtools para R para mostrar estadísticas descriptivas y curvas de densidad para dos distribuciones normales.
- Pase una sola columna de una hoja de cálculo de Minitab como entrada.
- Agregue un título de tabla.
- Agregue etiquetas de columna para una tabla.
- Envíe una tabla al panel Salida de Minitab.
- Cree un gráfico y envíelo al panel Salida de Minitab.
| Archivo | Descripción |
|---|---|
| bimodal.R | Secuencia de R comandos que toma una columna de una hoja de cálculo de Minitab, prueba la unimodalidad y produce resultados para una combinación de dos distribuciones normales si los datos no son unimodales. |
Todos los archivos a los que se hace referencia en esta guía están disponibles en este archivo .ZIP: r_guide_files.zip.
Prerrequisitos
-
El R script del siguiente ejemplo requiere los siguientes R paquetes:
- mtbr
- El R paquete que integra Minitab y R. En el ejemplo, las funciones de este módulo envían los resultados de R a Minitab. Para obtener información sobre cómo instalar el paquete de R Minitab, vaya al Paso 2:Instale mtbr.
- mixtools
- El R paquete que usa el script para crear la salida de una mezcla de distribuciones normales.
- diptest
- El R paquete que usa el script para probar si los datos son unimodales.
install.packages("mixtools")Para obtener ayuda con la instalación de paquetes, consulte con el departamento de R soporte técnico de su organización. El Soporte Técnico de Minitab no puede ayudar con la instalación de R paquetes.
Pasos para ejecutar el ejemplo
- Asegúrese de haber instalado los módulos necesarios: mtbr.
- Guarde el archivo de script de R, bimodal.R, en su ubicación predeterminada para archivos de Minitab. Para obtener más información sobre dónde busca Minitab los R archivos de script, vaya a Carpetas predeterminadas para archivos R para Minitab.
- Abra el conjunto de datos de muestra CostoEnergProceso.MWX.
-
En la sección Línea de
comandos de Minitab, ingrese
RSCR "bimodal.R" "Process 1". - Seleccione Corrida.
bimodal. R
# Load the necessary libraries
#Original code by Valentina Tillman
library(mixtools)
library(mtbr)
library(diptest)
# Retrieve sample data
input_column <- commandArgs(trailingOnly = TRUE)
data <- mtb_get_column(input_column)
dip_test_result <- dip.test(data)
if (dip_test_result$p.value < 0.05) {
# Fit a bimodal mixture model
bimodal_fit <- normalmixEM(data, k = 2)
# Manually extract parameter estimates and format them as a data frame
bimodal_table <- data.frame(
Mean = bimodal_fit$mu,
Standard_Deviation = bimodal_fit$sigma,
Proportion = bimodal_fit$lambda #tells you what % of the data is clustered around which mean. Also called lambda
)
# Define title and headers
mytitle <- "Modeling a Bimodal Distribution"
myheaders <- names(bimodal_table)
# Add the table to the mtbr output
mtb_add_table(columns = bimodal_table, headers = myheaders, title = mytitle)
png("r_bimodal_image.png")
plot(bimodal_fit, density = TRUE, which = 2)
graphics.off()
mtb_add_image("r_bimodal_image.png")
# Now generate tolerance intervals using the parameters found using mixtools
# Set the desired coverage level (e.g., 95%)
coverage_level <- 0.95
alpha <- 1 - coverage_level
# Calculate the tolerance intervals for each component
tolerance_intervals <- lapply(1:2, function(i) {
mu <- bimodal_fit$mu[i]
sigma <- bimodal_fit$sigma[i]
n <- bimodal_fit$lambda[i] # proportion of the component
# Calculate the critical value for the normal distribution
z <- qnorm(1 - alpha / (2 * n))
# Calculate lower and upper bounds of the tolerance interval
lower_bound <- mu - z * sigma
upper_bound <- mu + z * sigma
c(lower_bound, upper_bound)
})
# Show the tolerance intervals
tolerance_intervals_df <- data.frame(
Component = c("First Mode", "Second Mode"),
Lower_Bound = sapply(tolerance_intervals, "[", 1),
Upper_Bound = sapply(tolerance_intervals, "[", 2)
)
myheaders <- c("Component", "Lower Bound", "Upper Bound")
mytitle <- "Tolerance Intervals for Bimodal Distribution"
mtb_add_table(columns = tolerance_intervals_df, headers = myheaders, title = mytitle)
} else {
mtb_add_message("This data is unimodal.")
}
Resultados
Modeling a Bimodal Distribution
| Mean | Standard_Deviation | Proportion |
|---|---|---|
| 34.1875 | 1.50909 | 0.516129 |
| 48.3333 | 1.84992 | 0.483871 |
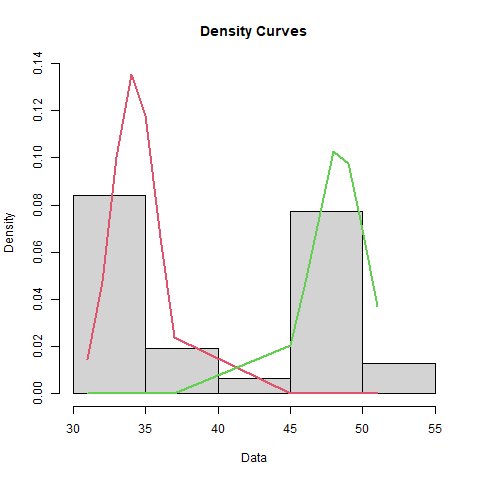
Tolerance Intervals for Bimodal Distribution
| Component | Lower Bound | Upper Bound |
|---|---|---|
| First Mode | 31.6821 | 36.6929 |
| Second Mode | 45.3200 | 51.3467 |
