Prueba exacta de Fisher
La prueba exacta de Fisher es una prueba de independencia. La prueba se basa en una distribución exacta y no en la distribución aproximada de chi-cuadrada que se utiliza para las pruebas de Pearson y de relación de verosimilitud pruebas. La prueba exacta de Fisher es útil cuando los conteos esperados de celda son bajos y la aproximación de chi-cuadrada no es muy buena.
Fórmula
- tamaño de la población
- número total de observaciones
- número de éxitos en la población
- número de observaciones en la primera fila
- Tamaño de muestra
- número de observaciones en la primera columna
Ejemplo
| Niño | Adulto | Total de filas | |
|---|---|---|---|
| Azúcar | 9 | 1 | 10 |
| Chispa Chocolate | 2 | 8 | 10 |
| Total de columnas | 11 | 9 | 20 |
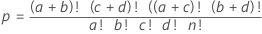
| Niño | Adulto | Total de filas | |
|---|---|---|---|
| Azúcar | a | b | a+b |
| Chispa Chocolate | c | d | c+d |
| Total de columnas | a+c | b+d | a+b+c+d |
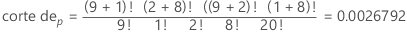
En este ejemplo, la suma de los valores p que son menores o iguales que el corte de p para las otras matrices posibles es 0.0054775.
Prueba exacta de McNemar
La prueba de McNemar compara las proporciones que se observan antes y después de un tratamiento. Por ejemplo, la prueba de McNemar se puede utilizar para determinar si un programa de capacitación cambia la proporción de participantes que contestan correctamente una pregunta.
Las observaciones de la prueba de McNemar se pueden resumir en una tabla de dos por dos, como se muestra abajo.
| Después del tratamiento | |||
| Antes del tratamiento | Condición verdadera | Condición no verdadera | Total |
| Condición verdadera | n11 | n12 | n1. |
| Condición no verdadera | n21 | n22 | n2. |
| Total | n·1 | n·2 | n·· |
La condición para el ejemplo de la capacitación es una respuesta correcta. Por lo tanto, n21 representa el número de participantes que contestan la pregunta correctamente después de la capacitación, pero no antes de la capacitación. Y n12 representa el número de participantes que contestan la pregunta correctamente antes de la capacitación, pero no después de la capacitación. El número total de participantes está representado por n...
Diferencia estimada
Sea δ la diferencia entre las probabilidades marginales, p1.- p.1, en la población. La diferencia estimada,  , viene dada por la siguiente fórmula:
, viene dada por la siguiente fórmula:
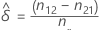
Intervalo de confianza
Un intervalo de confianza aproximado de 100(1 – α)% viene dado por la siguiente fórmula:

donde α es el nivel de significancia de la prueba, z α/2 es la puntuación z asociada a la probabilidad de cola de α/2 y EE viene dado por la siguiente fórmula:
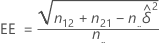
Valor p
La hipótesis nula es δ = 0. El valor p exacto para la prueba de la hipótesis nula se calcula como:

donde X es una variable aleatoria que se extrae de una distribución binomial con una probabilidad de evento de 0.5 y un número de ensayos igual a n21 + n12.
Prueba de Cochran-Mantel-Haenszel
La prueba presupone que no existe ninguna interacción de tres factores. El propósito de la prueba es evaluar el grado de relación entre dos variables dicotómicas, controlando al mismo tiempo una variable perturbadora. El estadístico CMH se compara con un percentil de chi-cuadrada con un grado de libertad.
La prueba de Cochran-Mantel-Haenszel (CMH) solo se aplica si existen tres o más variables de clasificación y las dos primeras variables tienen dos niveles cada una. Todas las variables más allá de las dos primeras se tratan como una sola variable Z a los efectos de la prueba CMH, tratándose cada combinación de niveles como un nivel de Z.
Fórmula
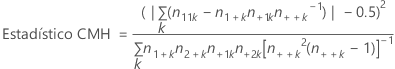
Notación
| Término | Description |
|---|---|
| k | nivel de Z |
| n11k | número de observaciones en la primera fila, primera columna |
| n1+k | número de observaciones en la primera fila |
| n+1k | número de observaciones en la primera columna |
| n++k | número total de observaciones |
| n2+k | número de observaciones en la segunda fila |
| n+2k | número de observaciones en la segunda columna |
