En este tema
Número de pares concordantes y discordantes
Un par es concordante si la observación que tiene una clasificación más alta en la variable X también se clasifica más alto en la variable Y. El par es discordante si la observación que tiene una clasificación más alta en la variable X se clasifica más bajo en Y. El par tiene valores iguales si los sujetos tienen la misma clasificación en X y/o en Y.
Fórmula


Notación
| Término | Description |
|---|---|
| nij | observaciones en la celda correspondiente a la iésima fila y la jésima columna |
Gamma
La gamma de Goodman y Kruskal es una medida de la asociación entre las variables ordinales. Existe asociación perfecta cuando |γ| = 1. Si X y Y son independientes, γ = 0.
Fórmula

Notación
| Término | Description |
|---|---|
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares discordantes = Σi<kΣj>l nij nkl |
| nij | observaciones en la celda correspondiente a la iésima fila y la jésima columna |
D de Somers
La D de Somers mide la fuerza y la dirección de la relación entre dos variables ordinales.
Fórmula
Con Y como la variable de respuesta:

Con X como la variable de respuesta:

Notación
| Término | Description |
|---|---|
| TX | número de pares con valores iguales en X = 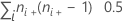 |
| TY | número de pares con valores iguales en Y = 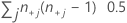 |
| C | número de pares concordantes |
| D | número de pares discordantes |
| ni+ | número de observaciones en la iésima fila |
| n+j | número de observaciones en la jésima columna |
| nij | observaciones en la celda correspondiente a la iésima fila y la jésima columna |
| n++ | número total de observaciones |
Tau-b de Kendall
La tau-b de Kendall, al igual que la gamma, mide la asociación entre las variables ordinales. Una fortaleza de la tau-b de Kendall como medida de asociación es que representa pares de valores iguales en su cálculo. La gamma tiene un problema con los pares de valores iguales, así que la gamma casi siempre muestra una mayor asociación que la tau-b. Los valores de la tau-b van desde -1.0 hasta 1.0.
Fórmula

Notación
| Término | Description |
|---|---|
| TX | número de pares con valores iguales en X = Σi ni+ (ni+- 1) 0.5 |
| TY | número de pares con valores iguales en Y = Σj n+j (n+j- 1) 0.5 |
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares discordantes = Σi<kΣj>l nij nkl |
| ni+ | número de observaciones en la iésima fila |
| n+j | número de observaciones en la jésima columna |
| nij | observaciones en la celda correspondiente a la iésima fila y la jésima columna |
| n++ | número total de observaciones |
Prueba de concordancia
La prueba de concordancia es una prueba de independencia. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades inferiores proporcionan mayor evidencia en contra de la hipótesis nula.
Fórmula
La prueba de concordancia utiliza un estadístico de prueba normal estándar:

El valor p es igual a la probabilidad de que Z sea mayor que Z*.
Notación
| Término | Description |
|---|---|
| C | número de pares concordantes = Σi<kΣj<l nij nkl |
| D | número de pares discordantes = Σi<kΣj>l nij nkl |
| SE(C-D) | Error estándar o C-D, que equivale aproximadamente a 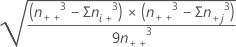 |
| n++ | el número total de observaciones |
| ni+ | el número de observaciones en la iésima fila. |
| n+j | El número de observaciones en la j-ésima columna. |
