Seleccione el método o la fórmula de su preferencia.
En este tema
Valor esperado para cada categoría
Fórmula
El valor esperado, E, para cada categoría, i, se calcula como:
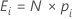
Notación
| Término | Description |
|---|---|
| pi | proporciones de la prueba para la iésima categoría, que es igual a 1/k o el valor que usted especifique |
| k | número de categorías distintas |
| N | total de valores observados (O1 + ... + Ok) |
| Oi | valor observado para la i ésima categoría |
Estadístico de prueba de chi-cuadrada
Fórmula
El estadístico de la prueba de chi-cuadrada se calcula como:
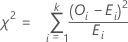
Notación
| Término | Description |
|---|---|
| k | número de categorías distintas |
| Oi | valor observado para la i ésima categoría |
| Ei | valor esperado para la iésima categoría |
Contribución al estadístico de chi-cuadrada
Fórmula
Contribución de la iésima categoría al valor de chi-cuadrada es:

Notación
| Término | Description |
|---|---|
| Oi | valor observado para la i ésima categoría |
| Ei | valor esperado para la iésima categoría |
Grados de libertad (GL)
Fórmula
Los grados de libertad (GL) se calculan como:

Notación
| Término | Description |
|---|---|
| GL | grados de libertad |
| k | número de categorías |
Valor p
Fórmula
El valor p se calcula como: Prob (Χ > Estadístico de prueba)
Notación
| Término | Description |
|---|---|
| X | sigue una distribución de chi-cuadrada con k – 1grados de libertad |
Ejemplo de cálculo
Dado lo siguiente:
| Categoría i | Observados Oi | Proporciones de prueba pi |
|---|---|---|
| A | 5 | 0.1 |
| B | 15 | 0.2 |
| C | 10 | 0.3 |
| D | 10 | 0.4 |
| N=40 |
Calculados:
| Categoría i | Valor esperado
Ei = (pi * N) |
Contribución a chi-cuadrada
(Oi- Ei)2 / Ei |
|---|---|---|
| A | 0.1 * 40 = 4 | (5 – 4)2 / 4 = 0.2500 |
| B | 0.2 * 40 = 8 | (15 – 8)2 / 8 = 6.1250 |
| C | 0.3 * 40 = 12 | (10 – 12)2 / 12 = 0.3333 |
| D | 0.4 * 40 = 16 | (10 – 16)2 / 16 = 2.2500 |
χ2 = 0.2500 + 6.1250 + 2.2500 + 0.3333 = 8.9583
GL = k – 1 = 3
Valor p = Prob (Χ > 8.9583) = 0.0299
Notación
| Término | Description |
|---|---|
| GL | grados de libertad |
| k | número de categorías |
