En este tema
Parámetro
El parámetro muestra el estadístico que usted seleccionó en el cuadro de diálogo. Los parámetros son medidas descriptivas de una población completa que se utilizan como las entradas para que una función de distribución de probabilidad (PDF, por sus siglas en inglés) genere curvas de distribución. Para obtener más información, vaya a ¿Qué son parámetros, estimaciones de parámetros y distribuciones de muestreo?.
Longitud de observación
Los procesos de Poisson cuentan las ocurrencias de un determinado evento o propiedad en un rango de observación específico, que puede representar cosas como tiempo, área, volumen y número de elementos. La longitud de observación representa la magnitud, duración o tamaño de cada rango de observación.
Interpretación
Minitab utiliza la longitud de observación para convertir la tasa de ocurrencia a una forma que sea más conveniente para su situación.
Por ejemplo, si cada observación de la muestra cuenta el número de eventos en un año, una longitud de 1 representa una tasa de ocurrencia anual, mientras que una longitud de 12 representa una tasa de ocurrencia mensual.
- El total de ocurrencias es 122, porque los inspectores encontraron 122 defectos.
- El tamaño de la muestra (N) es 50, porque los inspectores tomaron una muestra de 50 cajas.
- Para determinar el número de defectos por toalla, los inspectores utilizan una longitud de observación de 10 porque cada caja contiene 10 toallas. Para determinar el número de defectos por caja, los inspectores utilizan una longitud de observación de 1.
- La tasa de ocurrencia es (Total de ocurrencias / N) / (longitud de observación) = (122/50) / 10 = 0.244. Por lo tanto, cada toalla tiene 0.244 defectos.
Distribución
- Normal
-
La distribución normal es una distribución con forma de campana en la cual las desviaciones estándar sucesivas con respecto a la media establecen los valores de referencia para estimar el porcentaje de observaciones de los datos. Estos valores de referencia son la base de muchas pruebas de hipótesis, tales como las pruebas Z y t.
Por ejemplo, la estatura de todos los adultos masculinos que viven en el estado de Pennsylvania sigue aproximadamente una distribución normal. Por lo tanto, la estatura de la mayoría de los hombres está cerca de la estatura media de 69 pulgadas. Un número similar de hombres son un poco más altos y un poco más bajos que 69 pulgadas. Solo unos pocos son mucho más altos o mucho más bajos.
- Binomial
-
Cuando usted clasifica elementos, eventos o personas de manera independiente en una de dos categorías, entonces el número de elementos, eventos o personas en una categoría siguen la distribución binomial. Las dos categorías deben ser mutuamente excluyentes, como si/no, pasa/no pasa o defectuoso/no defectuoso.
Por ejemplo, unos ingenieros examinan una muestra de pernos para verificar si existen grietas notables que no permitan utilizarlos. Los pernos que no presentan grietas se clasifican como no defectuosos y los pernos que tienen grietas se clasifican como defectuosos.
- Poisson
-
Cuando usted cuenta la presencia de una característica, resultado o actividad en cierta cantidad de tiempo, área u otra longitud de observación, obtiene datos de Poisson. Los datos de Poisson se evalúan en conteos por unidad, con unidades del mismo tamaño.
Por ejemplo, los inspectores de una empresa de autobuses cuentan el número de averías de las unidades cada día durante 30 días.
Desviación estándar
La desviación estándar es la medida más común de dispersión, que indica qué tan dispersos están los datos con respecto a la media. El símbolo σ (sigma) suele utilizarse para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido. El valor que Minitab muestra es el valor de planificación que usted especificó en el cuadro de diálogo.
Proporción
Una proporción es una porción relativa de un todo, en oposición a un conteo o frecuencia. La proporción es igual al número de eventos dividido entre el tamaño de la muestra. El valor que Minitab muestra es el valor de planificación que usted especificó en el cuadro de diálogo.
Tasa
La tasa de ocurrencia de un evento es el número promedio de veces que ocurre el evento por cada unidad de duración de la observación. El valor que Minitab muestra es el valor de planificación que usted especificó en el cuadro de diálogo.
Media
La media de Poisson es el número promedio de veces que ocurre un evento durante el espacio total de observación. El valor que Minitab muestra es el valor de planificación que usted especificó en el cuadro de diálogo.
Nivel de confianza
Un nivel de confianza de 95% por lo general funciona adecuadamente. Esto indica que 19 de 20 muestras (95%) de la misma población producirán intervalos de confianza que contendrán el parámetro de población.
El nivel de confianza representa el porcentaje de intervalos que incluirían el parámetro de población si usted tomara muestras de la misma población una y otra vez. Por lo tanto, si recogió 100 muestras y creó 100 intervalos de confianza de 95%, cabría esperar que aproximadamente 95 de los intervalos incluyeran el parámetro de población, como por ejemplo la media de la población, como se muestra en la siguiente figura.
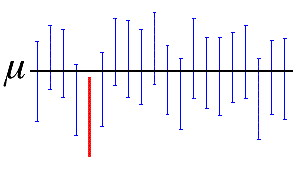
En la figura, la línea horizontal representa el valor fijo de la media desconocida de la población, µ. Los 19 intervalos de confianza azules verticales que se sobreponen a la línea horizontal contienen el valor de la media de la población. El único intervalo de confianza rojo que está completamente por debajo de la línea horizontal no lo contiene.
Intervalo de confianza
Minitab muestra el tipo de intervalo de confianza que usted especificó en el cuadro de diálogo.
El intervalo de confianza proporciona un rango de valores probables para la proporción de la población. Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces la muestra, un determinado porcentaje de los intervalos o límites de confianza resultantes contendría el parámetro de población desconocido. El porcentaje de estos intervalos o límites de confianza que contiene el parámetro es el nivel de confianza del intervalo.
Un límite superior define un valor en comparación con el cual es probable que el parámetro de población sea menor. Un límite inferior define un valor en comparación con el cual es probable que el parámetro de población sea mayor.
