En este tema
Nivel de significancia (α)
El nivel de significancia (denotado como alfa o α) es el máximo nivel aceptable de riesgo para un error tipo I.
Interpretación
Use el nivel de significancia para decidir si un efecto es estadísticamente significativo. Puesto que el nivel de significancia es el valor umbral de la significancia estadística, un valor más alto aumenta la probabilidad de cometer un error tipo I. Un error tipo I es la conclusión incorrecta de que un efecto es estadísticamente significativo.
Desviación estándar asumida
La desviación estándar asumida es la estimación de la desviación estándar de las mediciones de respuesta en corridas experimentales replicadas. Si ya realizó un análisis en Minitab que produjo una tabla ANOVA, puede utilizar la raíz cuadrada del cuadrado medio ajustado del error.
Interpretación
Utilice la desviación estándar asumida para describir qué tan variables son los datos. Valores más altos de la desviación estándar asumida indican más variación o "ruido" en los datos, lo cual hace que disminuya la potencia estadística de un diseño.
Factores
El número muestra cuántos factores hay en el diseño.
Interpretación
Utilice el número de factores para verificar que el diseño tenga todos los factores que usted necesita evaluar. Los factores son las variables que usted controla en el experimento. Los factores también se conocen como variables independientes, variables explicativas y variables predictoras. Para los cálculos de potencia y tamaño de la muestra, todos los factores son numéricos. Los factores numéricos utilizan pocos valores controlados en el experimento, aunque son posibles muchos valores. Estos valores se conocen como niveles de los factores.
Por ejemplo, usted estudia los factores que podrían afectar la resistencia del plástico durante el proceso de manufactura. Decide incluir Temperatura en su experimento. Puesto que la temperatura es un factor, solo hay tres valores de configuración de temperatura en el experimento: 100° C, 150° C y 200° C.
Diseño
El número muestra cuántos puntos de vértice hay en una réplica.
Interpretación
Utilice este número para identificar el diseño de Plackett-Burman que utilizan los cálculos de potencia. Un punto de vértice es una corrida experimental donde los factores están en sus niveles altos o bajos.
Puntos centrales
El número muestra cuántos puntos centrales hay en el diseño.
Interpretación
Utilice el número de puntos centrales para determinar el efecto de diferentes números de puntos centrales en los resultados. Los puntos centrales son corridas donde todos los factores se establecen en un punto intermedio entre sus niveles bajo y alto.
Los puntos centrales generalmente tienen poca influencia en los resultados cuando el diseño incluye réplicas de los puntos de vértice. Los puntos centrales tienen otros usos además de su influencia en los calculos de potencia. Por ejemplo, la prueba de curvatura en la respuesta requiere puntos centrales.
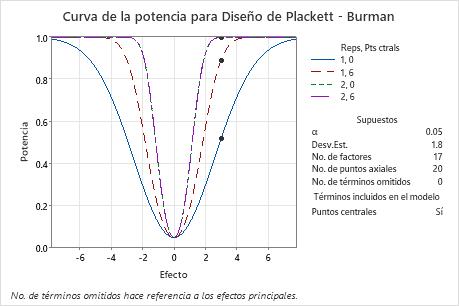
En estos resultados, los puntos en la curva de potencia muestran cálculos para una diferencia de 3. El diseño con 1 réplica y sin puntos centrales tiene una potencia cercana a 0.5. El diseño con 1 réplica y 6 puntos centrales tiene una potencia de casi 0.9. Con dos réplicas, las curvas de potencia para 0 puntos centrales y 6 puntos centrales no se distinguen en la gráfica. La curva para 6 puntos centrales es levemente más alta para los efectos distintos de cero. Ambos valores de potencia están cerca de 1.
Método
| Factores: | 17 | Diseño: | 20 |
|---|
Resultados
| Puntos centrales | Efecto | Reps | Corridas totales | Potencia |
|---|---|---|---|---|
| 0 | 3 | 1 | 20 | 0.517308 |
| 0 | 3 | 2 | 40 | 0.998927 |
| 6 | 3 | 1 | 26 | 0.889603 |
| 6 | 3 | 2 | 46 | 0.999082 |
Efecto
Si usted ingresa el número de réplicas, el valor de potencia y el número de puntos centrales, Minitab calcula el efecto. El efecto es la diferencia en la respuesta entre los niveles alto y bajo de un factor que usted desea que el diseño detecte. Esta diferencia es el resultado de un solo factor (efecto principal).
Interpretación
Utilice el tamaño del efecto para determinar la capacidad del diseño para detectar un efecto. Si usted ingresa un número de réplicas, una potencia y un número de puntos centrales, entonces Minitab calcula el tamaño del efecto más pequeño que el diseño puede detectar con la potencia especificada. Por lo general, con más réplicas, un experimento diseñado puede detectar efectos más pequeños.
En estos resultados, el diseño con una réplica puede detectar una diferencia de cerca de 0.015 con una potencia de 80%. La diferencia que el diseño puede detectar con una potencia de 90% es mayor que 0.015, alrededor de 0.018. El diseño con 2 réplicas puede detectar una diferencia que es menor que 0.015 con una potencia de 80%, alrededor de 0.007.
Método
| Factores: | 31 | Diseño: | 32 |
|---|---|---|---|
| Puntos centrales (total): | 4 |
Resultados
| Puntos centrales | Reps | Corridas totales | Potencia | Efecto |
|---|---|---|---|---|
| 4 | 1 | 36 | 0.8 | 0.0153027 |
| 4 | 1 | 36 | 0.9 | 0.0180278 |
| 4 | 2 | 68 | 0.8 | 0.0073261 |
| 4 | 2 | 68 | 0.9 | 0.0084775 |
Réplicas
Las réplicas son múltiples corridas experimentales con la misma configuración de factores.
Interpretación
Utilice el número de réplicas para estimar cuántas corridas experimentales debe incluir en el diseño. Si usted ingresa una potencia, el tamaño del efecto y el número de puntos centrales, Minitab calcula el número de réplicas. Puesto que los números de réplicas y puntos centrales se especifican en valores enteros, la potencia real puede ser mayor que el valor objetivo. Si usted aumenta el número de réplicas, la potencia del diseño también aumenta. Conviene incluir suficientes réplicas para lograr una potencia adecuada.
Puesto que las réplicas son valores enteros, los valores de potencia que usted especifica son valores objetivo de potencia. Los valores reales de potencia corresponden al número de réplicas y el número de puntos centrales en el experimento diseñado. Los valores reales de potencia son por lo menos tan grandes como los valores objetivo de potencia.
En estos resultados, Minitab calcula el número de réplicas para lograr la potencia objetivo. El diseño que detecta un efecto de 2 con una potencia de 0.8 requiere 1 réplica. Para alcanzar una potencia de 0.9, el diseño requiere 2 réplicas. La potencia real con 2 réplicas es mayor que 0.99. Esta potencia real es el menor valor de potencia que es mayor que o igual a 0.9 y que se puede obtener utilizando un número entero de réplicas. Para detectar el efecto menor de 0.9 con una potencia de 0.8, el diseño requiere 4 réplicas. Para detectar el efecto menor de 0.9 con una potencia de 0.9, el diseño requiere 5 réplicas.
Método
| Factores: | 15 | Diseño: | 32 |
|---|---|---|---|
| Puntos centrales (total): | 0 |
Resultados
| Puntos centrales | Efecto | Reps | Corridas totales | Potencia objetivo | Potencia real |
|---|---|---|---|---|---|
| 0 | 2.0 | 1 | 32 | 0.8 | 0.877445 |
| 0 | 2.0 | 2 | 64 | 0.9 | 0.995974 |
| 0 | 0.9 | 4 | 128 | 0.8 | 0.843529 |
| 0 | 0.9 | 5 | 160 | 0.9 | 0.914018 |
Total de corridas
Una corrida experimental es una combinación de los niveles de los factores que se utiliza para medir las respuestas. El número total de corridas es la cantidad de mediciones de la respuesta incluidas en el diseño. Múltiples ejecuciones de la misma combinación de niveles de los factores se consideran corridas experimentales separadas y se denominan réplicas.
Interpretación
Utilice el número total de corridas para verificar que el experimento diseñado tenga el tamaño adecuado para sus recursos. Para un diseño de Plackett-Burman, esta fórmula da el número total de corridas:

| Término | Description |
|---|---|
| n | Número de puntos de vértice por réplica |
| r | Número de réplicas |
| cptotal | Número de puntos centrales |
En estos resultados, un diseño con 12 puntos de vértice y 4 puntos centrales tiene un total de 16 corridas. El número de corridas en 2 réplicas del diseño es 12*2 + 4 = 28.
Método
| Factores: | 8 | Diseño: | 12 |
|---|---|---|---|
| Puntos centrales (total): | 4 |
Resultados
| Puntos centrales | Efecto | Reps | Corridas totales | Potencia |
|---|---|---|---|---|
| 4 | 2.5 | 1 | 16 | 0.523009 |
| 4 | 2.5 | 2 | 28 | 0.895399 |
Potencia
La potencia de un diseño es la probabilidad de que el diseño determine que un efecto es estadísticamente significativo. La diferencia entre las medias de la variable de respuesta en los niveles alto y bajo de un factor es el tamaño del efecto.
Interpretación
Utilice el valor de potencia para determinar la capacidad del diseño para detectar un efecto. Si usted ingresa un número de réplicas, un tamaño de efecto y un número de puntos centrales, entonces Minitab calcula la potencia del diseño. Por lo general, un valor de potencia de 0,9 se considera adecuado. Un valor de 0,9 indica que un diseño tiene una probabilidad de 90% de detectar un efecto del tamaño que especifique. Generalmente, mientras más bajo sea el número de réplicas, menor será la potencia. Si un diseño tiene poca potencia, es posible que usted no detecte un efecto y concluya erróneamente que no existe ninguno.
Estos resultados demuestran cómo un aumento en el número de corridas experimentales aumenta la potencia. Para un tamaño de efecto de 0,9, la potencia del diseño es aproximadamente 0,55 con un total de 64 corridas. Con un total de 160 corridas, la potencia del diseño aumenta a cerca de 0,91.
Estos resultados también demuestran cómo aumenta la potencia con un incremento en el tamaño del efecto. Para un diseño de 64 corridas, la potencia es aproximadamente 0,55 para un tamaño de efecto de 0,9. Con un tamaño de efecto de 1,5, la potencia aumenta a cerca de 0,93.
Método
| Factores: | 15 | Diseño: | 32 |
|---|---|---|---|
| Puntos centrales (total): | 0 |
Resultados
| Puntos centrales | Efecto | Reps | Corridas totales | Potencia |
|---|---|---|---|---|
| 0 | 1.5 | 5 | 160 | 0.999830 |
| 0 | 1.5 | 2 | 64 | 0.932932 |
| 0 | 0.9 | 5 | 160 | 0.914018 |
| 0 | 0.9 | 2 | 64 | 0.545887 |
Curva de potencia
La curva de potencia grafica la potencia del diseño versus el tamaño del efecto. El efecto se refiere a la diferencia entre el valor medio de la respuesta en los niveles alto y bajo de un factor.
Interpretación
Utilice la curva de potencia para evaluar las propiedades adecuadas para el diseño.
La curva de potencia representa la relación entre la potencia y el tamaño del efecto para todas las combinaciones de puntos centrales y réplicas. Cada símbolo de la curva de potencia representa un valor calculado con base en los valores que usted ingresa. Por ejemplo, si usted ingresa un número de réplicas, un valor de potencia y un número de puntos centrales, Minitab calcula el tamaño del efecto correspondiente y muestra el valor calculado en la gráfica para la combinación de réplicas y puntos centrales. Si desea determinar las réplicas o los puntos centrales, la gráfica también incluye curvas para otras combinaciones de réplicas y puntos centrales que se encuentran en las combinaciones que alcanzan la potencia objetivo. La gráfica no muestra curvas para casos que no poseen suficientes grados de libertad para evaluar la significancia estadística.
Examine los valores de la curva para determinar el tamaño del efecto que el experimento detecta con cierto valor de potencia, número de puntos de vértice y número de puntos centrales. Por lo general, un valor de potencia de 0.9 se considera adecuado. Sin embargo, algunos profesionales consideran que un valor de potencia de 0.8 funciona adecuadamente. Si un diseño tiene poca potencia, usted pudiera no detectar un efecto que sea significativo desde el punto de vista práctico. Al aumentar el número de réplicas, aumenta la potencia del diseño. Conviene incluir suficientes corridas experimentales en el diseño para lograr una potencia adecuada. Un diseño tiene más potencia para detectar un efecto más grande que un efecto más pequeño.
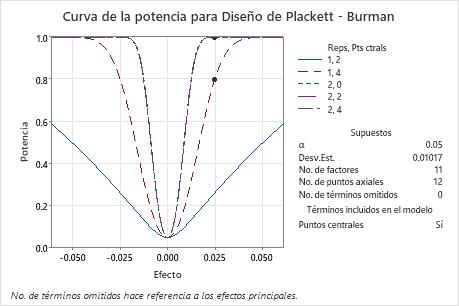
En estos resultados, Minitab calcula el número de réplicas para alcanzar una potencia objetivo de por lo menos 0.8 o 0.9 para un tamaño del efecto de 0.025. El experimento diseñado incluye 12 puntos de vértice para estudiar 11 factores. Los cálculos consideran experimentos diseñados con 0, 2 o 4 puntos centrales. La curva que muestra 1 réplica con 4 puntos centrales tiene un símbolo para el efecto de 0.25 donde la potencia es mayor que la potencia objetivo de 0.8. Las 3 curvas que representan los experimentos con 2 réplicas tienen símbolos que muestran que la potencia para detectar un efecto de 0.025 es mayor que la potencia objetivo de 0.9.
Puesto que existe una solución con 2 réplicas y 2 puntos centrales y existe una solución con 1 réplica y 4 puntos centrales, la gráfica también incluye una curva para un experimento con 1 réplica y 2 puntos centrales. Este experimento no alcanza ninguno de los dos valores de potencia objetivo para el efecto de 0.025, por lo que esta curva no muestra un símbolo. La gráfica no incluye la curva para 1 réplica con 0 puntos centrales, porque este experimento no cuenta con suficientes grados de libertad para evaluar la significancia estadística cuando se omiten 0 términos del modelo.
