Un ingeniero especializado en calidad planea un experimento diseñado para estudiar la transparencia de una pieza de plástico. Antes de realizar el experimento, el ingeniero desea asegurarse de que el experimento tenga una potencia adecuada. Planea examinar 10 factores numéricos. Para un diseño base, el ingeniero selecciona un diseño con 12 corridas experimentales y 3 puntos centrales. Desea poder detectar un efecto de 5 unidades de transparencia sin utilizar más de 4 réplicas. Experimentos anteriores indican que 4.5 es una estimación adecuada de la desviación estándar. El ingeniero decide calcular la potencia de un modelo con efectos principales y un término para puntos centrales.
- Elija .
- En Número de factores, ingrese 10.
- En Número de puntos axiales, seleccione 12.
- En Réplicas, ingrese 1 2 3 4.
- En Efectos, ingrese 5.
- En Número de puntos centrales, ingrese 3.
- En Desviación estándar, ingrese 4.5.
- Haga clic en Aceptar.
Interpretar los resultados
El diseño sin réplicas tiene una potencia de aproximadamente 30%. Con 3 réplicas y un total de 39 corridas, el diseño tiene una probabilidad de casi 90% de detectar un efecto importante. Con 4 réplicas y un total de 51 corridas, el diseño tiene más de 95% de probabilidad de detectar un efecto importante. La curva de potencia muestra la relación entre la potencia y el tamaño del efecto. Los símbolos en las curvas representan el tamaño del efecto de 5 que el ingeniero especificó. El ingeniero decide que el diseño de 3 réplicas proporciona suficiente potencia.
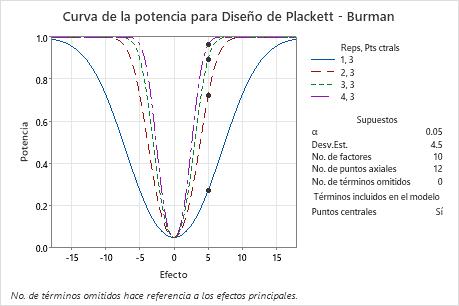
Método
| Factores: | 10 | Diseño: | 12 |
|---|---|---|---|
| Puntos centrales (total): | 3 |
Resultados
| Puntos centrales | Efecto | Reps | Corridas totales | Potencia |
|---|---|---|---|---|
| 3 | 5 | 1 | 15 | 0.272032 |
| 3 | 5 | 2 | 27 | 0.720550 |
| 3 | 5 | 3 | 39 | 0.894838 |
| 3 | 5 | 4 | 51 | 0.963485 |
