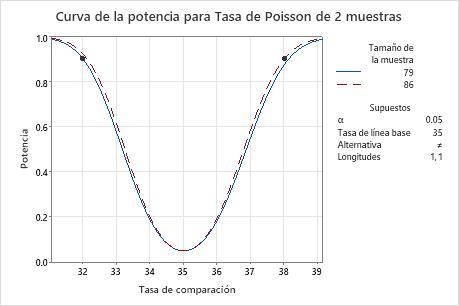
Un consultor de seguridad vial desea comparar el número de automóviles por hora que transitan por dos calles diferentes. Antes de recoger los datos para una prueba de tasa de Poisson de 2 muestras, el consultor utiliza un cálculo de potencia y tamaño de la muestra. El consultor desea determinar qué tan grande es el tamaño de la muestra que la prueba necesita para obtener una potencia de 0.9 y detectar una tasa de comparación de 32 o 38 (una diferencia de 3 con respecto a la tasa de línea base de 35).
- Elija .
- En Tasas de comparación (R1), ingrese 32 38.
- En Valores de potencia, ingrese 0.9.
- En Tasa de línea base (R2), ingrese 35.
- Haga clic en Aceptar.
Interpretar los resultados
Para detectar una tasa de comparación de 32 con un valor de potencia de 0.9, el consultor necesita un tamaño de muestra de 79. Para detectar una tasa de comparación de 38 con un valor de potencia de 0.9, el consultor necesita un tamaño de muestra de 86. El analista decide recopilar un tamaño de muestra de 86 para que la prueba tenga un valor de potencia de al 0.9 para ambas tasas de comparación. Puesto que el valor de potencia objetivo de 0.9 da como resultado un tamaño de muestra que no es un entero, Minitab también muestra la potencia (Potencia real) del tamaño de muestra redondeado.
Resultados
| Tasa de comparación | Tamaño de la muestra | Potencia objetivo | Potencia real |
|---|---|---|---|
| 32 | 79 | 0.9 | 0.902793 |
| 38 | 86 | 0.9 | 0.902550 |