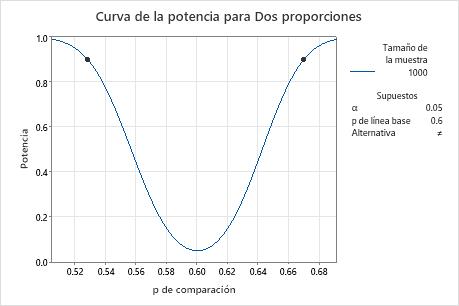
Un funcionario de la oficina de ayuda financiera de una universidad desea determinar si los estudiantes de sexo masculino o femenino tienen mayor probabilidad de conseguir empleo durante el verano. Los resultados de un estudio previo sugieren que 60% de los estudiantes consiguen empleo en el verano. Antes de recoger los datos para una prueba de 2 proporciones, el funcionario utiliza un cálculo de potencia y tamaño de la muestra para determinar qué tan pequeña es la diferencia que puede detectar la prueba cuando el tamaño de la muestra es 1,000 y la potencia es 0.9.
- Elija .
- En Tamaños de la muestra, ingrese 1000.
- En Valores de potencia, ingrese 0.9.
- En Proporción de línea base (p2), ingrese 0.6.
- Haga clic en Aceptar.
Interpretar los resultados
Con un tamaño de muestra de 1,000 y un valor de potencia de 0.9, el funcionario puede detectar una diferencia entre las proporciones de aproximadamente 7% en cualquier dirección. Esta diferencia es adecuada, por lo que el funcionario recopila los datos para el análisis de 2 proporciones.
Resultados
| Tamaño de la muestra | Potencia | p de comparación |
|---|---|---|
| 1000 | 0.9 | 0.669724 |
| 1000 | 0.9 | 0.528190 |