En este tema
Nivel de significancia (α)
El nivel de significancia (denotado como α o alfa) es el nivel máximo aceptable de riesgo de rechazar la hipótesis nula cuando la hipótesis nula es verdadera (error tipo I). El nivel de significancia también se interpreta como la potencia de la prueba cuando la hipótesis nula (H0) es verdadera. Por lo general, usted elige el nivel de significancia antes de analizar los datos. El nivel de significancia predeterminado es 0.05.
Interpretación
Utilice el nivel de significancia para minimizar el valor de potencia de la prueba cuando la hipótesis nula (H0) sea verdadera. Con valores más altos de nivel de significancia, la prueba tiene más potencia, pero también aumenta la probabilidad de cometer un error tipo I, que consiste en rechazar la hipótesis nula cuando es verdadera.
Longitud de observación
Los procesos de Poisson cuentan las ocurrencias de un determinado evento o propiedad en un rango de observación específico, que puede representar cosas como tiempo, área, volumen y número de elementos. La longitud de observación representa la magnitud, duración o tamaño de cada rango de observación.
Interpretación
Minitab utiliza la longitud de observación para convertir la tasa de ocurrencia a una forma que sea más conveniente para su situación.
Por ejemplo, si cada observación de la muestra cuenta el número de eventos en un año, una longitud de 1 representa una tasa de ocurrencia anual, mientras que una longitud de 12 representa una tasa de ocurrencia mensual.
- El total de ocurrencias es 122, porque los inspectores encontraron 122 defectos.
- El tamaño de la muestra (N) es 50, porque los inspectores tomaron una muestra de 50 cajas.
- Para determinar el número de defectos por toalla, los inspectores utilizan una longitud de observación de 10 porque cada caja contiene 10 toallas. Para determinar el número de defectos por caja, los inspectores utilizan una longitud de observación de 1.
- La tasa de ocurrencia es (Total de ocurrencias / N) / (longitud de observación) = (122/50) / 10 = 0.244. Por lo tanto, cada toalla tiene 0.244 defectos.
Tasa de comparación
La tasa de comparación es el valor que usted desea comparar con la tasa hipotética.
Interpretación
Minitab calcula la tasa de comparación. La diferencia entre la tasa de comparación y la tasa hipotética es la diferencia mínima para la que usted puede alcanzar el nivel especificado de potencia para cada tamaño de la muestra. Con tamaños de muestra más grandes, la prueba puede detectar diferencias más pequeñas. Lo que se busca es detectar la diferencia más pequeña que tiene consecuencias prácticas para la aplicación específica.
Para investigar más a fondo la relación entre el tamaño de la muestra y la tasa de comparación a una potencia específica, utilice la curva de potencia.
Tamaño de la muestra
El tamaño de la muestra es el número total de observaciones en la muestra.
Interpretación
Utilice el tamaño de la muestra para estimar cuántas observaciones necesita para obtener cierto valor de potencia para la prueba de hipótesis con una diferencia específica.
Minitab calcula qué tan grande debe ser la muestra para que una prueba con la potencia que usted especificó detecte la diferencia entre la tasa hipotética y la tasa de comparación. Debido a que los tamaños de las muestras son números enteros, la potencia real de la prueba pudiera ser levemente mayor que el valor de potencia que usted especifique.
Si usted aumenta el tamaño de la muestra, la potencia de la prueba también aumenta. Conviene tener suficientes observaciones en la muestra para lograr la potencia adecuada. Sin embargo, no debe tener un tamaño de muestra tan grande que le haga perder tiempo y dinero en un muestreo innecesario o detectar diferencias poco importantes para ser estadísticamente significativas.
Para investigar más a fondo la relación entre el tamaño de la muestra y la diferencia con una potencia específica, utilice la curva de potencia.
Potencia
La potencia de una prueba de hipótesis es la probabilidad de que la prueba rechace correctamente la hipótesis nula. La potencia de una prueba de hipótesis se ve afectada por el tamaño de la muestra, la diferencia, la variabilidad de los datos y el nivel de significancia de la prueba.
Para obtener más información, vaya a ¿Qué es potencia?.
Interpretación
Minitab calcula la potencia de la prueba con base en la tasa de comparación y tamaño de la muestra especificados. Por lo general, un valor de potencia de 0,9 se considera adecuado. Un valor de 0,9 indica que usted tiene una probabilidad de 90% de detectar una diferencia entre la tasa hipotética y la tasa de comparación de la población y el objetivo cuando realmente exista una diferencia. Si una prueba tiene poca potencia, usted podría no detectar una diferencia y concluir erróneamente que no existe ninguna. Generalmente, cuando el tamaño de la muestra es más pequeño o la diferencia es más pequeña, la prueba tiene menos potencia para detectar una diferencia.
Si usted ingresa una tasa de comparación y un valor de potencia para la prueba, entonces Minitab calcula qué tan grande debe ser la muestra. Minitab también calcula la potencia real de la prueba para ese tamaño de muestra. Debido a que los tamaños de las muestras son números enteros, la potencia real de la prueba pudiera ser levemente mayor que el valor de potencia que usted especifique.
Curva de potencia
La curva de potencia grafica la potencia de la prueba versus la tasa de comparación.
Interpretación
Utilice la curva de potencia para evaluar el tamaño de la muestra o la potencia adecuados para la prueba.
La curva de potencia representa todas las combinaciones de potencia y tasa de comparación para cada tamaño de muestra cuando el nivel de significancia se mantiene constante. Cada símbolo de la curva de potencia representa un valor calculado con base en los valores que usted ingresa. Por ejemplo, si usted ingresa un tamaño de muestra y un valor de potencia, Minitab calcula la proporción de comparación correspondiente y muestra el valor calculado en la gráfica.
Examine los valores de la curva para determinar la diferencia entre la tasa de comparación y la tasa hipotética que se puede detectar con cierto valor de potencia y tamaño de muestra. Por lo general, un valor de potencia de 0.9 se considera adecuado. Sin embargo, algunos profesionales consideran que un valor de potencia de 0.8 funciona adecuadamente. Si una prueba de hipótesis tiene poca potencia, usted pudiera no detectar una diferencia que sea significativa desde el punto de vista práctico. Si usted aumenta el tamaño de la muestra, la potencia de la prueba también aumenta. Conviene tener suficientes observaciones en la muestra para lograr la potencia adecuada. Sin embargo, no debe tener un tamaño de muestra tan grande que le haga perder tiempo y dinero en un muestreo innecesario o detectar diferencias poco importantes para ser estadísticamente significativas. Si reduce el tamaño de la diferencia que desea detectar, la potencia también disminuye.
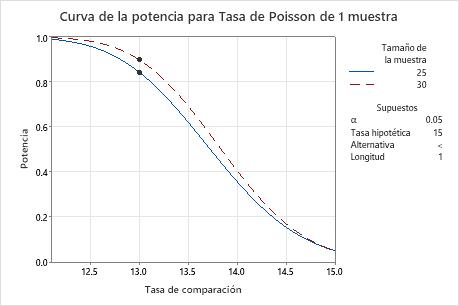
En esta gráfica, la curva de potencia para un tamaño de muestra de 25 indica que la prueba tiene una potencia de aproximadamente 0.84 para una tasa de comparación de 13. Para un tamaño de muestra de 30, la curva de potencia indica que la prueba tiene una potencia de aproximadamente 0.9 para una tasa de comparación de 13. A medida que la tasa de comparación se acerca a la tasa hipotética (15, en esta gráfica), la potencia de la prueba disminuye y se acerca al nivel de significancia (también denominado α), que es 0.05 para este análisis.