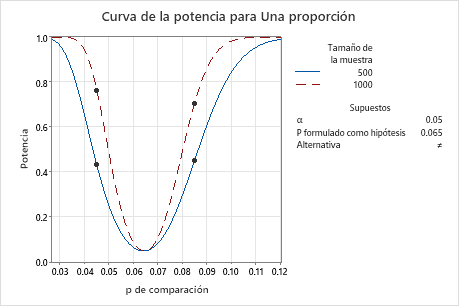
Un analista de mercadotecnia desea determinar si los anuncios enviados por correo a una muestra aleatoria de hogares da como resultado una tasa de respuesta que es diferente del promedio nacional de 6.5% (valor objetivo). Antes de recoger los datos para una prueba de 1 proporción, el analista utiliza un cálculo de potencia y tamaño de la muestra. El analista desea determinar cuál será la potencia de la prueba cuando el tamaño de la muestra sea 500 o 1000 y la prueba pueda detectar una proporción de comparación de 4.5% y 8.5%.
- Elija .
- En Tamaños de la muestra, ingrese 500 1000.
- En Proporciones de comparación, ingrese 0.045 0.085.
- En Proporción hipotética, ingrese 0.065.
- Haga clic en Aceptar.
Interpretar los resultados
Con un tamaño de muestra de 500, la prueba tendrá una potencia de 0.431 y 0.449 para detectar una proporción de comparación de 0.045 y 0.085. Con un tamaño de muestra de 1,000, la prueba tendría una potencia de 0.764 y 0.704 para detectar una proporción de comparación de de 0.045 y 0.085. El analista decide que 0.764 no es suficiente potencia y recolecta un tamaño de muestra mayor que 1,000.
Resultados
| p de comparación | Tamaño de la muestra | Potencia |
|---|---|---|
| 0.045 | 500 | 0.431131 |
| 0.045 | 1000 | 0.764259 |
| 0.085 | 500 | 0.449114 |
| 0.085 | 1000 | 0.703796 |