Una ingeniera que trabaja para un proveedor de productos oftalmológicos evalúa una nueva solución de limpieza para lentes de contacto. La ingeniera desea comprobar que la nueva solución limpia las lentes tan bien como la marca líder. La ingeniera pide a 14 participantes que usen las lentes de contacto durante un día y luego las limpien. Cada participante limpia una lente con la nueva solución y la otra lente con la marca líder. Para evaluar la limpieza de cada lente, la ingeniera mide el ángulo de contacto de una gota de líquido en la lente. El ángulo de contacto se ve afectado por cualquier película o depósitos en la lente. Para ser equivalentes, el ángulo medio de la nueva solución debe estar a no más de ±0.5 grados del ángulo medio de la marca líder.
Antes de recoger los datos para la prueba de equivalencia con datos pareados, la ingeniera utiliza un cálculo de potencia y tamaño de la muestra para determinar si un tamaño de muestra de 14 provee una potencia adecuada para la prueba. Con base en muestras previas, la ingeniera estima que la desviación estándar de la población es 0.42.
- Elija .
- En Hipótesis sobre, seleccione Media de prueba - media de referencia (Diferencia).
- En ¿Qué desea deteminar? (hipótesis alterna), seleccione Límite inferior < media de prueba - media de referencia < límite superior.
- En Límite inferior, ingrese -0.5. En Límite superior, ingrese 0.5.
- En Tamaños de la muestra, ingrese 14.
- En Diferencias (dentro de los límites), ingrese 0.1 0.2 0.3 0.4.
- En Desviación estándar de diferencias pareadas, ingrese 0.42.
- Haga clic en Aceptar.
Interpretar los resultados
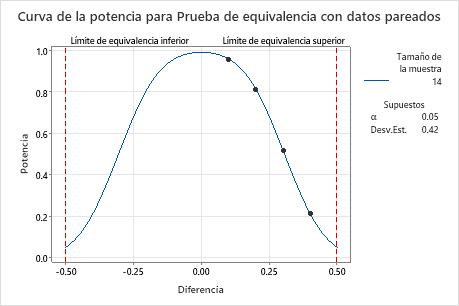
Si la diferencia es 0.1 y el ingeniero utiliza un tamaño de muestra de 14 pares de observaciones, entonces la potencia de la prueba es mayor que 0.9. Si la diferencia es 0.2 y el ingeniero utiliza un tamaño de muestra de 14 pares de observaciones, entonces la prueba tiene una potencia por encima de 0.8. Sin embargo, si la diferencia es 0.3 y el ingeniero utiliza un tamaño de muestra de 14 pares de observaciones, entonces la prueba tiene una potencia de aproximadamente 0.52, que no es adecuada.
Cuando la diferencia está más cerca del límite de equivalencia superior (0.5), la potencia de la prueba es más baja. Por ejemplo, para una diferencia de 0.4, si el ingeniero utiliza un tamaño de muestra de 14 pares de observaciones, entonces la prueba tiene una potencia de aproximadamente 0.22.
Para cualquier tamaño de muestra, a medida que la diferencia se acerca al límite de equivalencia inferior o al límite de equivalencia superior, la potencia de la prueba disminuye y se acerca al nivel de significancia (α, que es el riesgo de afirmar que existe equivalencia cuando no es cierto).
Método
| Potencia para diferencia: | Media de la prueba - media de referencia |
|---|---|
| Hipótesis nula: | Diferencia ≤ -0.5 o diferencia ≥ 0.5 |
| Hipótesis alterna | -0.5 < diferencia < 0.5 |
| Nivel α: | 0.05 |
Resultados
| Diferencia | Tamaño de la muestra | Potencia |
|---|---|---|
| 0.1 | 14 | 0.957371 |
| 0.2 | 14 | 0.811858 |
| 0.3 | 14 | 0.517255 |
| 0.4 | 14 | 0.211869 |