En este tema
Potencia para la diferencia
La primera línea de la salida indica cómo se especifican las hipótesis para la prueba de equivalencia.
"Power for difference" (Potencia para la diferencia) indica que las hipótesis se especifican en términos de la diferencia entre la media de la población de la prueba y la media de la población de referencia (Media de la prueba – media de referencia).
Potencia para la relación
La primera línea de la salida indica cómo se especifican las hipótesis para la prueba de equivalencia.
"Power for ratio" (Potencia para relación) indica que las hipótesis se especifican en términos de la relación entre la media de la población de la prueba y la media de la población de referencia por transformación logarítmica (Media de la prueba / media de referencia).
Hipótesis nula e hipótesis alternativa
- Hipótesis nula
- Minitab prueba una o las dos hipótesis nulas siguientes, dependiendo de la hipótesis alternativa que usted seleccionó:
- La diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es mayor que o igual al límite de equivalencia superior.
- La diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es menor que o igual al límite de equivalencia inferior.
- Hipótesis alternativa
- La hipótesis alternativa establece una o las dos hipótesis siguientes:
- La diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es menor que el límite de equivalencia superior.
- La diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es mayor que el límite de equivalencia inferior.
Interpretación
Utilice las hipótesis nula y alternativa para verificar que los criterios de equivalencia sean correctos y que seleccionó la hipótesis alternativa adecuada para la prueba.
Método
| Potencia para diferencia: | Media de la prueba - media de referencia |
|---|---|
| Hipótesis nula: | Diferencia ≤ -1 o diferencia ≥ 1 |
| Hipótesis alterna | -1 < diferencia < 1 |
| Nivel α: | 0.05 |
| Desviación estándar asumida | 0.41 |
- La diferencia entre la media de la población de la prueba y la media de la población de referencia es menor que o igual al límite de equivalencia inferior de −1.
- La diferencia entre la media de la población de la prueba y la media de la población de referencia es mayor que o igual al límite de equivalencia superior de 1.
Nivel de significancia (α)
El nivel de significancia (denotado por alfa o α) es el nivel máximo aceptable de riesgo de rechazar la hipótesis nula cuando la hipótesis nula es verdadera (error tipo I). Por ejemplo, si usted realiza una prueba de equivalencia utilizando las hipótesis predeterminadas, un α de 0.05 indica un riesgo de 5% de afirmar que existe equivalencia cuando la diferencia entre la media de la prueba y la media de referencia no se encuentre realmente dentro de los límites de equivalencia.
El nivel de significancia (α) para una prueba de equivalencia también determina el nivel de confianza del intervalo de confianza. El nivel de confianza es (1 – α) x 100% por opción predeterminada. Si usted utiliza el método alternativo para calcular el intervalo de confianza, el nivel de confianza es (1 – 2α) x 100%.
Interpretación
Utilice el nivel de significancia para minimizar el valor de potencia de la prueba cuando la hipótesis nula (H0) sea verdadera. Con valores más altos de nivel de significancia, la prueba tiene más potencia, pero también aumenta la probabilidad de cometer un error tipo I, que consiste en rechazar la hipótesis nula cuando es verdadera.
Desviación estándar asumida
La desviación estándar es la medida más común de dispersión, que indica qué tanto varían los datos con respecto a la media. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
Interpretación
La desviación estándar asumida es una estimación de planificación de la desviación estándar de la población que usted ingresa para el análisis de potencia. Minitab utiliza la desviación estándar asumida para calcular la potencia de la prueba. Valores más altos de la desviación estándar indican que hay más variación en los datos, lo cual hace que disminuya la potencia estadística de una prueba.Diferencia
Este valor representa la diferencia entre la media de la población de la prueba y la media de la población de referencia.
Nota
Las definiciones e interpretación incluidas en este tema se aplican a una prueba de equivalencia estándar que utilice la hipótesis alternativa predeterminada (Límite inferior < media de prueba - media de referencia < límite superior).
Interpretación
Si usted ingresa el tamaño de la muestra y la potencia de la prueba, entonces Minitab calcula la diferencia que la prueba puede detectar con la potencia y tamaño de la muestra especificados. Para tamaños de muestra más grandes, la diferencia puede estar más cerca de los límites de equivalencia.
Para investigar más a fondo la relación entre el tamaño de la muestra y la diferencia que la prueba puede detectar con una potencia dada, utilice la curva de potencia.
Método
| Potencia para diferencia: | Media de la prueba - media de referencia |
|---|---|
| Hipótesis nula: | Diferencia ≤ -1 o diferencia ≥ 1 |
| Hipótesis alterna | -1 < diferencia < 1 |
| Nivel α: | 0.05 |
| Desviación estándar asumida | 0.41 |
Resultados
| Tamaño de la muestra | Potencia | Diferencia |
|---|---|---|
| 8 | 0.9 | -0.368540 |
| 8 | 0.9 | 0.368540 |
| 12 | 0.9 | -0.494285 |
| 12 | 0.9 | 0.494285 |
| 20 | 0.9 | -0.613616 |
| 20 | 0.9 | 0.613616 |
Estos resultados muestran cómo al incrementar el tamaño de la muestra, aumenta el tamaño de la diferencia que se puede detectar con un nivel de potencia dado:
- Con 8 observaciones en cada grupo, la potencia de la prueba es al menos 0.9 cuando la diferencia se encuentra entre aproximadamente −0.37 y 0.37.
- Con 12 observaciones en cada grupo, la potencia de la prueba es al menos 0.9 cuando la diferencia se encuentra entre aproximadamente −0.49 y 0.49.
- Con 20 observaciones en cada grupo, la potencia de la prueba es al menos 0.9 cuando la diferencia se encuentra entre aproximadamente −0.61 y 0.61.
Relación
Este valor representa la relación de la media de la población de la prueba a la media de la población de referencia. Para realizar cálculos de potencia para una relación, debe seleccionar una hipótesis sobre Media de prueba / media de referencia (Relación, por transformación logarítmica).
Nota
Las definiciones e interpretación incluidas en este tema se aplican a una prueba de equivalencia que utilice la hipótesis alternativa predeterminada para la relación (Límite inferior < media de prueba / media de referencia < límite superior).
Interpretación
Si usted ingresa el tamaño de la muestra y la potencia de la prueba, entonces Minitab calcula las relaciones mínima y máxima que la prueba puede detectar con la potencia y tamaño de la muestra especificados. Para tamaños de muestra más grandes, la relación puede estar más cerca de los límites de equivalencia.
Para investigar más a fondo la relación entre el tamaño de la muestra y las relaciones que la prueba puede detectar con una potencia dada, utilice la curva de potencia.
Método
| Potencia para relación: | Media de la prueba / media de referencia |
|---|---|
| Hipótesis nula: | Relación ≤ 0.9 o Relación ≥ 1.1 |
| Hipótesis alterna | 0.9 < relación < 1.1 |
| Nivel α: | 0.05 |
| Coeficiente de variación asumido: | 0.09 |
Resultados
| Tamaño de la muestra | Potencia | Relación |
|---|---|---|
| 10 | 0.9 | * |
| 25 | 0.9 | 0.97060 |
| 25 | 0.9 | 1.01999 |
| 35 | 0.9 | 0.95897 |
| 35 | 0.9 | 1.03235 |
Estos resultados muestran cómo al incrementar el tamaño de la muestra, aumenta el rango de las relaciones que se puede detectar con un nivel de potencia dado:
- Con 10 observaciones en cada grupo, la prueba no puede alcanzar una potencia de 0.9 para ninguna relación.
- Con 25 observaciones en cada grupo, la potencia de la prueba es al menos 0.9 cuando la relación se encuentra entre aproximadamente 0.97 y 1.02.
- Con 35 observaciones en cada grupo, la potencia de la prueba es al menos 0.9 cuando la relación se encuentra entre aproximadamente 0.96 y 1.03.
Tamaño de la muestra
El tamaño de la muestra es el número total de observaciones en la muestra. Para una prueba de equivalencia de 2 muestras, el tamaño de la muestra se refiere al número de observaciones en cada uno de los dos grupos.
Interpretación
Utilice el tamaño de la muestra para estimar cuántas observaciones necesita para obtener cierto valor de potencia para la prueba de equivalencia con una diferencia específica.
Si usted ingresa una diferencia (o relación) y un valor de potencia para la prueba, entonces Minitab calcula qué tan grande debe ser la muestra.Debido a que los tamaños de las muestras son números enteros, la potencia real de la prueba pudiera ser levemente mayor que el valor de potencia que usted especifique.
Si usted aumenta el tamaño de la muestra, la potencia de la prueba también aumenta. Conviene tener suficientes observaciones en la muestra para lograr la potencia adecuada. Sin embargo, no debe tener un tamaño de muestra tan grande que le haga perder tiempo y dinero en un muestreo innecesario o detectar diferencias poco importantes para ser estadísticamente significativas.
Para investigar más a fondo la relación entre el tamaño de la muestra y la diferencia (o relación) que la prueba puede detectar con una potencia dada, utilice la curva de potencia.
Método
| Potencia para diferencia: | Media de la prueba - media de referencia |
|---|---|
| Hipótesis nula: | Diferencia ≤ -1 o diferencia ≥ 1 |
| Hipótesis alterna | -1 < diferencia < 1 |
| Nivel α: | 0.05 |
| Desviación estándar asumida | 0.41 |
Resultados
| Diferencia | Tamaño de la muestra | Potencia objetivo | Potencia real |
|---|---|---|---|
| 0.5 | 13 | 0.9 | 0.915407 |
| 0.7 | 33 | 0.9 | 0.902461 |
| 0.9 | 289 | 0.9 | 0.900360 |
Estos resultados muestran que, a medida que el tamaño de la diferencia aumenta y se acerca al valor del límite de equivalencia, se necesita un tamaño de muestra más grande para alcanzar una potencia dada. Si la diferencia es 0.5, entonces usted necesita 13 observaciones en cada grupo para alcanzar una potencia de 0.9. Con un tamaño de muestra de 13, usted logra una potencia de aproximadamente 0.92. Si la diferencia es 0.9, necesita al menos 289 observaciones en cada grupo para alcanzar una potencia de 0.9.
Potencia
La potencia de una prueba de equivalencia es la probabilidad de que la prueba demuestre que la diferencia (o relación) está dentro de los límites de equivalencia, cuando eso sea cierto. La potencia de una prueba de equivalencia se ve afectada por el tamaño de la muestra, la diferencia, los límites de equivalencia, la variabilidad de los datos y el nivel de significancia de la prueba.
Para obtener más información, vaya a Potencia para las pruebas de equivalencia.
Interpretación
Si usted ingresa un tamaño de la muestra y una diferencia (o relación), entonces Minitab calcula la potencia de la prueba. Por lo general, un valor de potencia de 0,9 se considera adecuado. Una potencia de 0,9 indica que usted tiene una probabilidad de 90% de demostrar equivalencia cuando la diferencia (o relación) entre las medias de las poblaciones está realmente dentro de los límites de equivalencia. Si una prueba de equivalencia tiene poca potencia, usted pudiera no demostrar equivalencia incluso cuando la media de la prueba y la media de referencia sean equivalentes.
Si usted ingresa una diferencia (o relación) y un valor de potencia para la prueba, entonces Minitab calcula qué tan grande debe ser la muestra. Minitab también calcula la potencia real de la prueba para ese tamaño de muestra. Debido a que los tamaños de las muestras son números enteros, la potencia real de la prueba pudiera ser levemente mayor que el valor de potencia que usted especifique.
Generalmente, cuando el tamaño de la muestra es más pequeño o cuando la diferencia (o relación) está más cerca de un límite de equivalencia, la prueba tiene menos potencia para afirmar que existe equivalencia.
Método
| Potencia para diferencia: | Media de la prueba - media de referencia |
|---|---|
| Hipótesis nula: | Diferencia ≤ -1 o diferencia ≥ 1 |
| Hipótesis alterna | -1 < diferencia < 1 |
| Nivel α: | 0.05 |
| Desviación estándar asumida | 0.41 |
Resultados
| Diferencia | Tamaño de la muestra | Potencia |
|---|---|---|
| 0.5 | 8 | 0.749766 |
| 0.5 | 15 | 0.946583 |
| 0.5 | 25 | 0.995405 |
| 0.8 | 8 | 0.236964 |
| 0.8 | 15 | 0.366456 |
| 0.8 | 25 | 0.522098 |
En estos resultados, un tamaño de muestra de 8 proporciona una potencia de aproximadamente 0.75 para una diferencia de 0.5. Sin embargo, el mismo tamaño de muestra proporciona una potencia de aproximadamente 0.24 para una diferencia de 0.8. En cada valor de la diferencia, aumentar el tamaño de la muestra aumenta la potencia de la prueba.
Curva de potencia
La curva de potencia grafica la potencia de la prueba versus la diferencia (o relación) entre la media de la prueba y la media de referencia.
Interpretación
Utilice la curva de potencia para evaluar el tamaño de la muestra o la potencia adecuados para la prueba.
La curva de potencia representa todas las combinaciones de potencia y diferencia (o relación) para cada tamaño de muestra cuando el nivel de significancia y la desviación estándar (o el coeficiente de variación) se mantienen constantes. Cada símbolo de la curva de potencia representa un valor calculado con base en los valores que usted ingresa. Por ejemplo, si usted ingresa un tamaño de muestra y un valor de potencia, Minitab calcula la diferencia (o relación) correspondiente y muestra el valor calculado en la gráfica.
Examine los valores de la curva para determinar la diferencia (o relación) entre la media de la prueba y la media de referencia que se puede detectar con cierto valor de potencia y tamaño de muestra. Por lo general, un valor de potencia de 0.9 se considera adecuado. Sin embargo, algunos profesionales consideran que un valor de potencia de 0.8 funciona adecuadamente. Si una prueba de equivalencia tiene poca potencia, usted pudiera no demostrar equivalencia incluso cuando las medias de las poblaciones sean equivalentes. Si usted aumenta el tamaño de la muestra, la potencia de la prueba también aumenta. Conviene tener suficientes observaciones en la muestra para lograr la potencia adecuada. Sin embargo, no debe tener un tamaño de muestra tan grande que le haga perder tiempo y dinero en un muestreo innecesario o detectar diferencias poco importantes para ser estadísticamente significativas. Normalmente, cuando las diferencias (o relaciones) están más cerca de los límites de equivalencia, se requiere más potencia para demostrar la equivalencia.
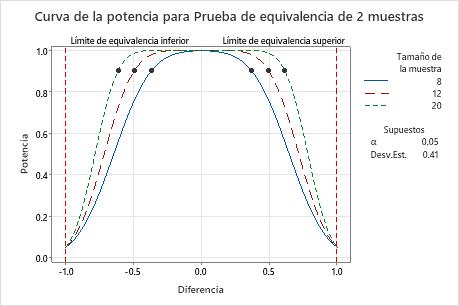
En esta gráfica, la curva de potencia para un tamaño de muestra de 8 (en cada grupo) indica que la prueba tiene una potencia de 0.9 para una diferencia de aproximadamente ±0.4. La curva de potencia para un tamaño de muestra de 12 indica que la prueba tiene una potencia de 0.9 para una diferencia de aproximadamente ±0.5. La curva de potencia para un tamaño de muestra de 12 indica que la prueba tiene una potencia de 0.9 para una diferencia de aproximadamente ±0.6. Para cada curva, a medida que la diferencia se acerca al límite de equivalencia inferior o al límite de equivalencia superior, la potencia de la prueba disminuye y se acerca al nivel de significancia (α, que es el riesgo de afirmar que existe equivalencia cuando no es cierto).
