Un ingeniero de empaques desea poner a prueba un nuevo método para sellar bolsas de refrigerios. La fuerza necesaria para abrir las bolsas no debería diferir en más de 10% del valor objetivo de 4.2 N (Newtons). Antes de recoger los datos para una prueba de equivalencia de 1 muestra, el ingeniero utiliza un cálculo de potencia y tamaño de la muestra para determinar qué tan grande debe ser la muestra para obtener una potencia de 80% (0.8). Con base en muestras previas, el ingeniero estima que la desviación estándar de la población es 0.332.
- Elija .
- En ¿Qué desea deteminar? (hipótesis alterna), elija Límite inferior < media de prueba - objetivo < límite superior.
- En Límite inferior, ingrese –0.42. En Límite superior, ingrese 0.42.
- En Diferencias (dentro de los límites), ingrese 0 0.1 0.2 0.3.
- En Valores de potencia, ingrese 0.8.
- En Desviación estándar, ingrese 0.332.
- Haga clic en Aceptar.
Interpretar los resultados
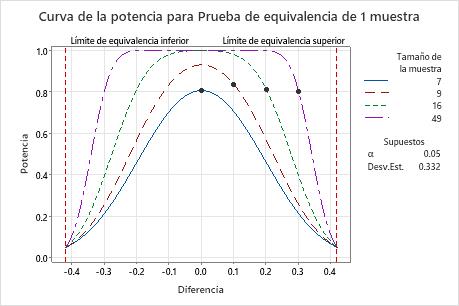
Si la diferencia es 0 (la fuerza media se encuentra en el objetivo), entonces el ingeniero necesita un tamaño de muestra de 7 para alcanzar una potencia de 0.8. Si el ingeniero utiliza un tamaño de muestra de 9, la potencia de la prueba está por encima de 0.9 para una diferencia de 0.
Cuando la diferencia está más cerca del límite de equivalencia superior (0.42), el ingeniero necesita un tamaño de muestra más grande para alcanzar la misma potencia. Por ejemplo, para una diferencia de 0.3, el ingeniero necesita un tamaño de muestra de 49 para alcanzar una potencia de 0.8.
Para cualquier tamaño de muestra, a medida que la diferencia se acerca al límite de equivalencia inferior o al límite de equivalencia superior, la potencia de la prueba disminuye y se acerca al nivel de significancia (α, que es el riesgo de afirmar que existe equivalencia cuando no es cierto).
Método
| Potencia para diferencia: | Media de la prueba - objetivo |
|---|---|
| Hipótesis nula: | Diferencia ≤ -0.42 o diferencia ≥ 0.42 |
| Hipótesis alterna | -0.42 < diferencia < 0.42 |
| Nivel α: | 0.05 |
| Desviación estándar asumida | 0.332 |
Resultados
| Diferencia | Tamaño de la muestra | Potencia objetivo | Potencia real |
|---|---|---|---|
| 0.0 | 7 | 0.8 | 0.805075 |
| 0.1 | 9 | 0.8 | 0.834590 |
| 0.2 | 16 | 0.8 | 0.811465 |
| 0.3 | 49 | 0.8 | 0.802154 |