En este tema
Estadístico de prueba
- Minitab jerarquiza las dos muestras combinadas. Minitab asigna el rango 1 a la observación más pequeña, el rango 2 a la segunda observación más pequeña, y así sucesivamente.
- Si hay dos o más observaciones iguales, Minitab asigna el rango promedio a las dos observaciones.
- Minitab suma los rangos de la primera muestra.
Jerarquizar valores iguales
- Ordenar las observaciones en orden ascendente.
- Asignar rangos a cada observación como si no hubiera empates.
- Para un conjunto de empates, sacar el promedio de los rangos correspondientes y asignar ese valor como el nuevo rango a cada valor igual de ese conjunto.
Ejemplo
Una muestra tiene 9 observaciones: 2.4, 5.3, 2.4, 4.0, 1.2, 3.6, 4.0, 4.3 y 4.0.
| Observación | Rango
(presuponiendo que no hay empates) |
Rango | |
|---|---|---|---|
| 1.2 | 1 | 1 | |
| Empate | 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 | |
| 3.6 | 4 | 4 | |
| Empate | 4.0 | 5 | 6 |
| 4.0 | 6 | 6 | |
| 4.0 | 7 | 6 | |
| 4.3 | 8 | 8 | |
| 5.3 | 9 | 9 |
- El número del conjunto de empates es 2.
- El número de valores iguales que están en el primer conjunto es 2
- El número de valores iguales que están en el segundo conjunto es 3.
Valor p
Fórmula
La prueba de Mann-Whitney utiliza un método de aproximación a la normal para determinar el valor p de la prueba.
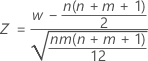está distribuido aproximadamente como una distribución normal con una media de 0 y una desviación estándar de 1, N(0,1).
| Hipótesis alternativa | Valor p |
|---|---|
| H1: η1 > η2 |  |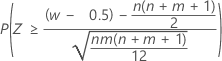
| H1: η1 < η2 |  |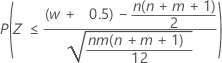
| H1: η1 ≠ η2 |  |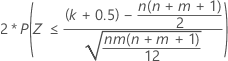
El valor p ajustado por lo general es más exacto que el valor p sin ajustar. Sin embargo, el valor p sin ajustar es el cálculo más conservador, porque siempre es mayor que el valor p ajustado para un determinado par de muestras.
Notación
| Término | Description |
|---|---|
| W | Estadísticos de la prueba de Mann-Whitney |
| n | tamaño de la muestra 1 |
| m | tamaño de la muestra 2 |
| η1 | mediana de la muestra 1 |
| η2 | mediana de la muestra 2 |
| k |  |
| i | 1, 2, …, I |
| I | número de conjuntos de empates |
| ti | número de valores iguales en el iésimo conjunto de empates |
Estimación de punto
El algoritmo de aproximación que Minitab utiliza para calcular la estimación de punto de η1 – η2 se describe en este artículo: J.W. McKean y T.A. Ryan, Jr. (1977). "An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem", Transactions on Mathematical Software, 183–185.
Intervalo de confianza
El intervalo de confianza de η1 – η2 se define como el rango de valores de η1 – η2 para el cual la hipótesis nula no es rechazada.
El método que Minitab utiliza para calcular el intervalo de confianza se describe en este artículo: J.W. McKean y T.A. Ryan, Jr. (1977). "An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem", Transactions on Mathematical Software, pp.183-185.
