En este tema
S
El estadístico de prueba tiene aproximadamente una distribución de chi-cuadrada (χ2) con grados de libertad asociados (k – 1). Si los datos de uno o más bloques tienen empates, Minitab utiliza el rango promedio e imprime un estadístico de prueba que se ha corregido para los empates. Para mayores detalles sobre este método, véase M. Hollander y D.A. Wolfe (1973)1.
Fórmula
Para calcular el estadístico de la prueba de chi-cuadrada, Minitab jerarquiza los datos por separado dentro de cada bloque y suma los rangos de cada tratamiento.
Si los datos no tienen empates, la fórmula es:
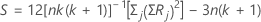
Si los datos tienen empates, la fórmula es:

donde C es un factor de corrección que es igual a:
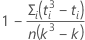
Notación
| Término | Description |
|---|---|
| j | 1, 2, ..., k |
| k | el número de condiciones del tratamiento |
| n | el número de bloques |
| Rj | la suma de los rangos para el tratamiento j |
| i | 1, 2, ..., m |
| m | el número de conjuntos de empates |
| ti | número de puntuaciones iguales en el iésimo conjunto de empates |
- M. Hollander y D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc.
Mediana principal
Para entender cómo calcular los efectos del tratamiento, las medianas de bloque y la mediana principal, consideremos los siguientes datos.
| Bloque | ||||
| Tratamiento | 1 | 2 | 3 | 4 |
| 1 | 0.15 | 0.26 | 0.23 | 0.99 |
| 2 | 0.55 | 0.26 | −0.22 | 0.99 |
| 3 | 0.55 | 0.66 | 0.77 | 0.99 |
Para calcular los efectos del tratamiento (método de Doksum1), primero encuentre la mediana de las diferencias entre los pares de tratamientos. Las diferencias en parejas para el tratamiento 1 menos el tratamiento 2 son 0.15 - 0.55 = −0.4, 0.26 – 0.26 = 0, 0.23 – (−0.22) = 0.45 y 0.99 – 0.99 = 0. La mediana de las diferencias es 0. Al realizar este cálculo para las otras dos parejas, se obtiene −0.4 para el tratamiento 1 menos el tratamiento 3 y −0.2 para el tratamiento 2 menos el tratamiento 3.
El efecto de cada tratamiento es el promedio de la mediana de las diferencias de ese tratamiento con todos los otros tratamientos (incluyendo el propio tratamiento). Para los datos de este ejemplo, efecto(2) = [mediana (2 – 1) + mediana (2 – 2) + mediana (2 – 3)]/3 = (0.00 + 0.00 – 0.20)/3 = −0.0667. Del mismo modo, efecto(1) = −0.1333 y efecto(3) = 0.20.
Para calcular las medianas ajustadas de bloque, ajuste cada observación restando el efecto del tratamiento apropiado a la observación. Las medianas ajustadas de bloque son simplemente las medianas de estos datos ajustados, calculadas dentro de cada bloque. La mediana principal es la mediana de las medianas ajustadas del bloque. La mediana estimada para cada nivel de tratamiento es el efecto del tratamiento más la mediana principal.
- M. Hollander y D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc., pp. 158 – 161.
Jerarquizar valores iguales
- Ordenar las observaciones en orden ascendente.
- Asignar rangos a cada observación como si no hubiera empates.
- Para un conjunto de empates, sacar el promedio de los rangos correspondientes y asignar ese valor como el nuevo rango a cada valor igual de ese conjunto.
Ejemplo
Una muestra tiene 9 observaciones: 2.4, 5.3, 2.4, 4.0, 1.2, 3.6, 4.0, 4.3 y 4.0
| Observación | Rango (presuponiendo que no hay empates) | Rango |
|---|---|---|
| 1.2 | 1 | 1 |
| 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 |
| 3.6 | 4 | 4 |
| 4.0 | 5 | 6 |
| 4.0 | 6 | 6 |
| 4.0 | 7 | 6 |
| 4.3 | 8 | 8 |
| 5.3 | 9 | 9 |
- El número de conjuntos de empates = 2.
- El número de valores iguales en el primer conjunto = 2
- El número de valores iguales en el segundo conjunto = 3.
