Soporte de Minitab® 

Métodos y fórmulas para Media de la prueba / media de referencia para Prueba de equivalencia con datos pareados

Más información sobre Minitab
Los siguientes métodos y fórmulas se utilizan para probar la relación entre la media de la prueba y la media de referencia.

En este tema

Relación

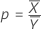
Notación

TérminoDescription
ρRelación
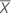Media de la prueba
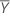Media de referencia

Límites de equivalencia

Sea k1 el valor que usted especifica para el límite inferior y k2 el valor que especifica para el límite superior. Por opción predeterminada, el límite de equivalencia inferior, δ1, viene dado por:

y el límite de equivalencia superior, δ2, viene dado por:

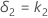
Grados de libertad (GL)

Notación

TérminoDescription
vGrados de libertad
nNúmero de pares de observaciones

S12

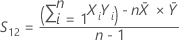
S12 representa la covarianza de la muestra entre los valores de X y los valores de Y. Este valor se utiliza en los cálculos del IC y los valores t.

Notación

TérminoDescription
XiLa iésima observación en la muestra de la prueba, tal que (Xi, Yi) sea el iésimo par de observaciones
YiLa iésima observación en la muestra de referencia, tal que (Xi, Yi) sea el iésimo par de observaciones
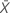Media de la muestra de la prueba
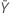Media de la muestra de referencia
nNúmero de pares de observaciones

Intervalo de confianza

Minitab no puede calcular el intervalo de confianza (IC) si se cumple cualquiera de las dos condiciones siguientes:

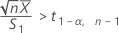
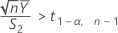
Si se cumplen las condiciones, Minitab calcula el IC con base en el método utilizado para el análisis.
  • IC de 100(1 - α)%

    Por opción predeterminada, Minitab calcula el IC de 100(1 - α)% para ρ de la siguiente manera:

    IC = [mín(C, ρL), máx(C, ρU)]

    donde:
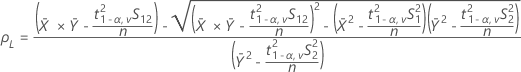
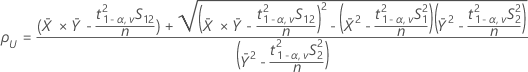
  • IC de 100(1 - 2α)%

    Si selecciona la opción para usar el IC de 100(1 - 2 α)%, entonces el IC viene dado por lo siguiente:

    IC = [ρL, ρU]
  • Intervalos unilaterales

    Para una hipótesis de Media de prueba / media de referencia > límite inferior, el límite inferior de 100(1 - α)% es igual a ρL.

    Para una hipótesis de Media de prueba / media de referencia < límite superior, el límite superior de 100(1 - α)% es igual a ρU.

Notación

TérminoDescription
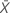Media de la muestra de la prueba
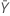Media de la muestra de referencia
S12Covarianza de la muestra entre los valores de X y los valores de Y
S1Desviación estándar de la muestra de la prueba
nel tamaño de la muestra
S2Desviación estándar de la muestra de referencia
δ1Límite de equivalencia inferior
δ2Límite de equivalencia superior
vGrados de libertad
αNivel de significancia de la prueba (alfa)
t1-α,vValor crítico superior 1 - α para una distribución t con v grados de libertad

Valores t

Sea t1 el valor t de la hipótesis y sea t2 el valor t de la hipótesis , donde es la relación de la media de la población de la prueba a la media de la población de referencia.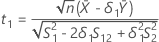

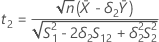
Notación

TérminoDescription
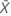Media de la muestra de la prueba
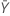Media de la muestra de referencia
S1Desviación estándar de la muestra de la prueba
S2Desviación estándar de la muestra de referencia
S12Correlación entre los valores de X y los valores de Y
nNúmero de pares de observaciones
δ1Límite de equivalencia inferior
δ2Límite de equivalencia superior
ΛRelación desconocida de la media de la población de la prueba a la media de la población de referencia

Valores p

La probabilidad, PH0, de cada hipótesis nula viene dada por la siguiente fórmula:

Si , entonces:

H0 Valor p

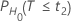Notación

TérminoDescription
ΛRelación desconocida de la media de la población de la prueba a la media de la población de referencia
δ1Límite de equivalencia inferior
δ2Límite de equivalencia superior
vGrados de libertad
TDistribución t con v grados de libertad
t1 Valor t de la hipótesis
t2 Valor t de la hipótesis
Nota

Para obtener información sobre cómo se calculan los valores t, véase la sección sobre valores t.

Copyright © 2024 Minitab, LLC. All rights Reserved.