Gráfica de equivalencia
Una gráfica de equivalencia muestra los límites de equivalencia, el intervalo de confianza para equivalencia y la decisión de si se puede afirmar que existe equivalencia.
Interpretación
Utilice la gráfica de equivalencia para ver un resumen gráfico de los resultados de la prueba y determinar si puede afirmar que existe equivalencia.
Compare el intervalo de confianza con los límites de equivalencia. Si el intervalo de confianza está completamente dentro de los límites de equivalencia, usted puede afirmar que la media de la población de la prueba es equivalente a la media de la población de referencia. Si parte del intervalo de confianza está fuera de los límites de equivalencia, no puede afirmar equivalencia.
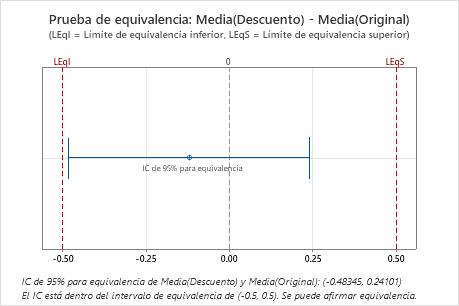
En estos resultados, el intervalo de confianza de 95% está completamente dentro del intervalo de equivalencia definido por el límite de equivalencia inferior (LEI) y el límite de equivalencia superior (LES). Por lo tanto, usted puede concluir que la media de la prueba es equivalente a la media de referencia.
Histograma
Un histograma divide los valores de la muestra en muchos intervalos y representa la frecuencia de los valores de los datos en cada intervalo con una barra.
Interpretación
Utilice histogramas para evaluar la forma y dispersión de los datos. Los histogramas funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Determine si sus datos parecen ser asimétricos.Cuando los datos son asimétricos, la mayoría de los datos se ubica hacia la parte superior o inferior de la gráfica. A menudo, es más fácil identificar la asimetría con una gráfica de caja o un histograma.
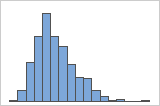
Asimétrico hacia la derecha
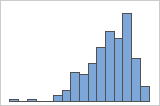
Asimétrico hacia la izquierda
Por ejemplo, el histograma con asimetría hacia la derecha muestra datos sobre salario. Muchos empleados reciben una cantidad relativamente pequeña, mientras que cada vez menos empleados reciben grandes salarios. El histograma con asimetría a la izquierda muestra datos de tasa de falla. Unos pocos elementos fallan antes, mientras que un número creciente de elementos falla posteriormente.
Los datos que son marcadamente asimétricos pueden afectar la validez de los resultados de la prueba si su muestra es pequeña (< 20 valores). Si sus datos son marcadamente asimétricos y tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son puntos de datos que están muy alejados de la mayoría de los demás datos, pueden afectar considerablemente sus resultados. Es más fácil identificar los valores atípicos en una gráfica de caja.
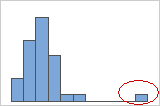
En un histograma, barras aisladas en los extremos sugieren posibles valores atípicos.
Usted debe tratar de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los datos que estén asociados a causas especiales y repetir el análisis. Para obtener más información sobre las causas especiales, vaya a Uso de gráficas de control para detectar la variación de causa común y la variación por causas especiales.
Gráfica del perfil del sujeto
Muestra la respuesta al tratamiento de referencia y al tratamiento de la prueba de cada participante en el estudio.
Interpretación
Utilice la gráfica del perfil del sujeto para examinar las respuestas de cada participante al tratamiento de la prueba y al tratamiento de referencia.
Verifique que el patrón general concuerde con los resultados de la prueba de equivalencia. Identifique cualquier sujeto cuya respuesta sea notablemente diferente de las demás respuestas, lo que podría afectar los resultados generales.
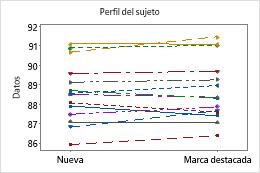
Esta gráfica del perfil del sujeto muestra que la mayoría de los participantes del estudio respondieron de manera similar al tratamiento de la prueba y al tratamiento de referencia. Ninguno de los tratamientos parece estar asociado de manera constante con una respuesta mayor o menor. Los resultados en la gráfica concuerdan con los resultados de la prueba (no se muestran), lo que indica que los dos tratamientos son equivalentes. Además, ninguna respuesta individual difiere considerablemente de las demás respuestas.
Gráfica de caja
La gráfica de caja proporciona un resumen gráfico de la distribución de las diferencias pareadas que muestra su variabilidad y tendencia central.
Interpretación
Utilice una gráfica de caja para examinar la dispersión de los datos e identificar cualquier posible valor atípico. Las gráficas de caja funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Determine si sus datos parecen ser asimétricos.Cuando los datos son asimétricos, la mayoría de los datos se ubica hacia la parte superior o inferior de la gráfica. A menudo, es más fácil identificar la asimetría con una gráfica de caja o un histograma.
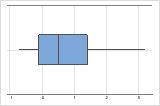
Asimétrico hacia la derecha
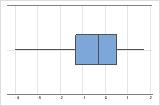
Asimétrico hacia la izquierda
Por ejemplo, la gráfica de caja con asimetría hacia la derecha muestra datos sobre salario. Muchos empleados reciben una cantidad relativamente pequeña, mientras que cada vez menos empleados reciben grandes salarios. La gráfica de caja con asimetría a la izquierda muestra datos de tasa de falla. Unos pocos elementos fallan antes, mientras que un número creciente de elementos falla posteriormente.
Los datos que son marcadamente asimétricos pueden afectar la validez de los resultados de la prueba si su muestra es pequeña (< 20 valores). Si sus datos son marcadamente asimétricos y tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son puntos de datos que están muy alejados de la mayoría de los demás datos, pueden afectar considerablemente sus resultados. Es más fácil identificar los valores atípicos en una gráfica de caja.
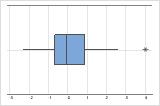
En una gráfica de caja, los valores atípicos se identifican con asteriscos (*).
Usted debe tratar de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los datos que estén asociados a causas especiales y repetir el análisis. Para obtener más información sobre las causas especiales, vaya a Uso de gráficas de control para detectar la variación de causa común y la variación por causas especiales.
