En este tema
Relación
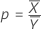
Notación
| Término | Description |
|---|---|
| ρ | Relación |
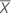 | Media de la prueba |
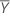 | Media de referencia |
Medias y desviaciones estándar
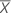, viene dada por:
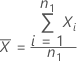
La media de la muestra de referencia,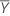 
, viene dada por:
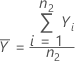
La desviación estándar de la muestra de la prueba, S1, viene dada por:
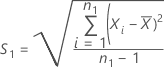
La desviación estándar de la muestra de referencia, S2, viene dada por:
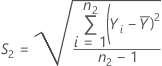
Notación
| Término | Description |
|---|---|
| X i | Observaciones de la muestra de la prueba, con i = 1, ..., n1 |
| Y i | Observaciones de la muestra de referencia, con i = 1, ..., n2 |
| n1 | Número de observaciones en la muestra de la prueba |
| n2 | Número de observaciones en la muestra de referencia |
Límites de equivalencia
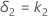
Sea k1 el valor que usted especifica para el límite inferior y k2 el valor que especifica para el límite superior. Por opción predeterminada, el límite de equivalencia inferior, δ1, viene dado por:
y el límite de equivalencia superior, δ2, viene dado por:
Grados de libertad (GL)
No asumir varianzas iguales (opción predeterminada)
Por opción predeterminada, los grados de libertad, v, vienen dados por la siguiente fórmula:
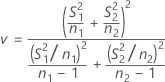
Minitab muestra v redondeado hacia abajo al valor entero más cercano.
Asumir varianzas iguales
Si selecciona la opción para asumir varianzas iguales, entonces Minitab calcula los grados de libertad de la siguiente manera:
Notación
| Término | Description |
|---|---|
| S1 | Desviación estándar de la muestra de la prueba |
| n1 | Número de observaciones en la muestra de la prueba |
| S2 | Desviación estándar de la muestra de referencia |
| n2 | Número de observaciones en la muestra de referencia |
Desviación estándar agrupada
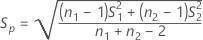
Notación
| Término | Description |
|---|---|
| Sp | Desviación estándar agrupada |
| S1 | Desviación estándar de la muestra de la prueba |
| n1 | Número de observaciones en la muestra de la prueba |
| S2 | Desviación estándar de la muestra de referencia |
| n2 | Número de observaciones en la muestra de referencia |
Intervalo de confianza
Minitab no puede calcular el intervalo de confianza (IC) si no se cumple ninguna de las tres condiciones siguientes:
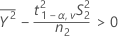
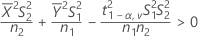
No asumir varianzas iguales (opción predeterminada)
- IC de 100(1 - α)%
Por opción predeterminada, Minitab calcula el IC de 100(1 - α)% para ρ de la siguiente manera:
IC = [mín(C, ρL), máx(C, ρU)]
donde:
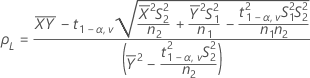
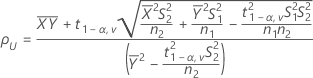
- IC de 100(1 - 2α)%
Si selecciona la opción para usar el IC de 100(1 - 2 α)%, entonces el IC viene dado por la siguiente fórmula:
IC = [ρL, ρU]
Asumir varianzas iguales
Si selecciona la opción para asumir varianzas iguales, entonces el IC se calcula de la siguiente manera.
Minitab no puede calcular el IC si no se cumple ninguna de las tres condiciones siguientes:
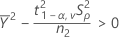
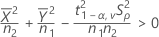
- IC de 100(1 -α)%
Minitab calcula el IC de 100(1 - α)% de la siguiente manera:
IC = [mín(C, ρL, máx(C, ρU)]
Donde: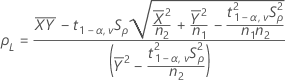
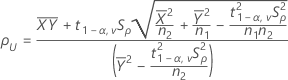
- IC de 100(1 - 2 α)%
Si selecciona la opción para usar el IC de 100(1 - 2 α)%, entonces el IC viene dado por la siguiente fórmula:
IC = (ρL, ρU)
Intervalos unilaterales
Para una hipótesis de Media de prueba / media de referencia > límite inferior, la banda inferior de 100(1 - α)% es igual a ρL.
Para una hipótesis de Media de prueba / media de referencia < límite superior, la banda superior de 100(1 - α)% es igual a ρU.
Notación
| Término | Description |
|---|---|
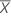 | Media de la muestra de la prueba |
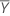 | Media de la muestra de referencia |
| S1 | Desviación estándar de la muestra de la prueba |
| n1 | Número de observaciones en la muestra de la prueba |
| S2 | Desviación estándar de la muestra de referencia |
| n2 | Número de observaciones en la muestra de referencia |
| δ1 | Límite de equivalencia inferior |
| δ2 | Límite de equivalencia superior |
| Sρ | Desviación estándar agrupada |
| v | Grados de libertad |
| α | Nivel de significancia de la prueba |
| t1-α,v | Valor crítico superior de 1 – α para una distribución t con v grados de libertad |
Valores t
No asumir varianzas iguales (opción predeterminada)
Sea t1 el valor t de la hipótesis
y sea t2 el valor t de la hipótesis 
, donde Λ es la relación de la media de la población de la prueba a la
media de la población de referencia. Por opción predeterminada, los valores t se
calculan de la siguiente manera: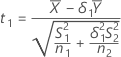 
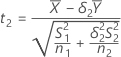
Asumir varianzas iguales
Si selecciona la opción para asumir varianzas iguales, entonces los valores t se calculan de la siguiente manera: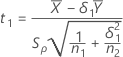
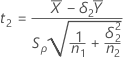
Notación
| Término | Description |
|---|---|
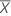 | Media de la muestra de la prueba |
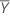 | Media de la muestra de referencia |
| S1 | Desviación estándar de la muestra de la prueba |
| n1 | Número de observaciones en la muestra de la prueba |
| S2 | Desviación estándar de la muestra de referencia |
| n2 | Número de observaciones en la muestra de referencia |
| Sρ | Desviación estándar agrupada |
| δ1 | Límite de equivalencia inferior |
| δ2 | Límite de equivalencia superior |
Valores p
Si 
, entonces:
| H0 | Valor p |
|---|---|
 |
 |
 |
 |
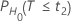Notación
| Término | Description |
|---|---|
| Λ | Relación desconocida de la media de la población de la prueba a la media de la población de referencia |
| δ1 | Límite de equivalencia inferior |
| δ2 | Límite de equivalencia superior |
| v | Grados de libertad |
| T | Distribución t con v grados de libertad |
| t1 | Valor t de la hipótesis  |
| t2 | Valor t de la hipótesis  |
Nota
Para obtener información sobre cómo se calculan los valores t, véase la sección sobre valores t.
