En este tema
Diferencia
Si usted seleccionó una hipótesis sobre la diferencia entre las medias, Minitab muestra la diferencia entre la media de la prueba y la media de referencia de sus muestras.
Interpretación
La media de la muestra de la prueba es una estimación de la media de la población de la prueba. La media de la muestra de referencia es una estimación de la media de la población de referencia. Por lo tanto, la diferencia entre las medias de la muestra proporciona una estimación de la diferencia entre la media de la población de la prueba y la media de la población de referencia.
Puesto que la diferencia se basa en datos de muestras y no en las poblaciones completas, usted no puede estar seguro de que sea igual a la diferencia entre la media de la población de la prueba y la media de la población de referencia. Para evaluar la precisión de la estimación para las poblaciones, puede utilizar un intervalo de confianza.
Relación
Si usted seleccionó una hipótesis sobre la relación de las medias, Minitab calcula la relación de la media de la muestra de la prueba a la media de la muestra de referencia.
Interpretación
La media de la muestra de la prueba es una estimación de la media de la población de la prueba. La media de la muestra de referencia es una estimación de la media de la población de referencia. Por lo tanto, la relación de las medias de la muestra proporciona una estimación de la relación de la media de la población de la prueba a la media de la población de referencia.
Puesto que la relación se basa en datos de muestras y no en las poblaciones completas, usted no puede estar seguro de que sea igual a la relación de la población. Para evaluar la precisión de la estimación para las poblaciones, puede utilizar un intervalo de confianza.
EE
El error estándar (EE) de la diferencia estima la variabilidad de la diferencia entre la media de la prueba y la media de referencia que usted obtendría si tomara muestras repetidas de las mismas poblaciones. El error estándar de la diferencia estima la variabilidad entre las muestras, mientras que la desviación estándar mide la variabilidad dentro de una misma muestra.
Por ejemplo, supongamos que usted tiene una diferencia entre la media de la prueba de la muestra y la media de referencia de la muestra de −0.12122 unidades. La muestra de la prueba de 10 valores de datos tiene una desviación estándar de 0.26138. La muestra de referencia de 9 valores de datos tiene una desviación estándar de 0.58064. El error estándar de la diferencia es igual a la raíz cuadrada de la suma (0.58064/10 + 0.26138/9) o 0.20324. Si usted recolectara múltiples muestras aleatorias del mismo tamaño y de la misma población, la desviación estándar de las diferencias entre las muestras sería aproximadamente 0.20324.
Interpretación
Utilice el error estándar de la diferencia para determinar el grado de precisión con el que la diferencia entre las medias de la prueba estima la diferencia entre la media de la población de la prueba y la media de la población de referencia.
Valores más bajos del error estándar indican una estimación más precisa. Por lo general, una desviación estándar más grande da como resultado un mayor error estándar de la diferencia y una estimación menos precisa. Un mayor tamaño de la muestra da como resultado un menor error estándar de la diferencia y una estimación más precisa.
Minitab utiliza el error estándar de la diferencia para calcular los estadísticos de la prueba (valores t).
Intervalo de confianza (IC)
El intervalo de confianza proporciona un rango de valores probables para la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia. El límite de confianza inferior define un valor en comparación con el cual es probable que la diferencia (o relación) sea mayor. El límite de confianza superior define un valor en comparación con el cual es probable que la diferencia (o relación) sea menor.
Nota
Si usted realiza una prueba de equivalencia utilizando la configuración predeterminada, Minitab muestra un intervalo de confianza para la equivalencia. Si cambia la configuración predeterminada y usa el método alternativo para calcular el intervalo de confianza, Minitab muestra un intervalo de confianza estándar. Para obtener información sobre la diferencia entre estos intervalos, vaya a Intervalos de confianza en pruebas de equivalencia.
Interpretación
Compare el intervalo de confianza con los límites de equivalencia. Si el intervalo de confianza está completamente dentro de los límites de equivalencia, usted puede afirmar que la media de la población de la prueba es equivalente a la media de la población de referencia. Si parte del intervalo de confianza está fuera de los límites de equivalencia, no puede afirmar equivalencia.
Diferencia: Media(Descuento) - Media(Original)
| Diferencia | EE | IC de 95% para equivalencia | Intervalo de equivalencia |
|---|---|---|---|
| -0.12122 | 0.20324 | (-0.483449, 0.241005) | (-0.5, 0.5) |
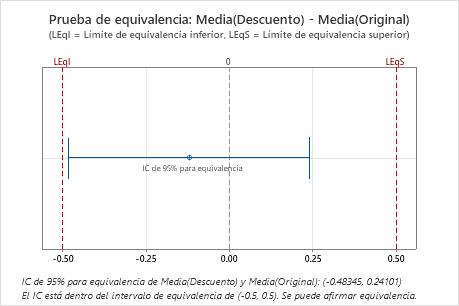
En estos resultados, el intervalo de confianza de 95% está completamente dentro del intervalo de equivalencia definido por el límite de equivalencia inferior (LEI) y el límite de equivalencia superior (LES). Por lo tanto, usted puede concluir que la media de la prueba es equivalente a la media de referencia.
Intervalo de equivalencia
Un intervalo de equivalencia es un rango de valores que están lo suficientemente cerca de la media de referencia como para considerarlos equivalentes. El intervalo se basa en su conocimiento del producto o proceso y es definido por un límite de equivalencia inferior (LEL) y un límite de equivalencia superior (UEL).
Interpretación
Compare el intervalo de confianza con los límites de equivalencia. Si el intervalo de confianza está completamente dentro de los límites de equivalencia, usted puede afirmar que la media de la población de la prueba es equivalente a la media de la población de referencia. Si parte del intervalo de confianza está fuera de los límites de equivalencia, usted no puede afirmar equivalencia.
Diferencia: Media(Genérico) - Media(Marca)
| Diferencia | EE | IC de 95% para equivalencia | Intervalo de equivalencia |
|---|---|---|---|
| -0.32104 | 0.060641 | (-0.427349, 0) | (-0.425035, 0.425035) |
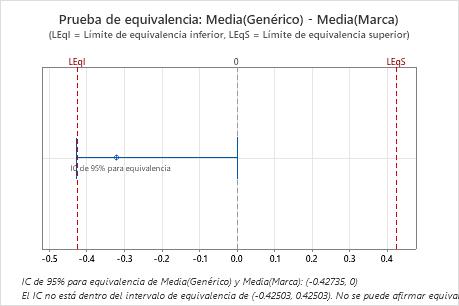
En estos resultados, el intervalo de confianza de 95% no está completamente dentro del intervalo de equivalencia definido por el límite de equivalencia inferior (LEL) y el límite de equivalencia superior (UEL). El borde inferior del intervalo de confianza se extiende más allá del límite de equivalencia inferior. Por lo tanto, usted no puede concluir que la media de la prueba es equivalente a la media de referencia.
Límite inferior
Minitab muestra una banda de confianza inferior si usted selecciona una hipótesis alternativa que solo incluye un límite inferior para la diferencia (o relación). La banda inferior indica un valor en comparación con el cual es probable que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia sea mayor.
Interpretación
Utilice la banda de confianza inferior para determinar si la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es mayor que el límite inferior. Si la banda de confianza inferior es mayor que el límite inferior, usted puede afirmar que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es mayor el límite inferior.
Diferencia: Media(Genérico) - Media(Marca)
| Diferencia | EE | Límite inferior de 95% | Límite inferior |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.42735 | -0.42503 |
En estos resultados, la banda de confianza inferior de 95% para la diferencia es −0.42735, que es menor que el límite inferior de −0.42503. Por lo tanto, usted no puede afirmar que la diferencia entre la media de la población de la prueba y la media de la población de referencia es mayor que el límite inferior.
Límite superior
Minitab muestra una banda de confianza superior si usted selecciona una hipótesis alternativa que solo incluye un límite superior para la diferencia (o relación). La banda superior indica un valor en comparación con el cual es probable que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia sea menor.
Interpretación
Utilice la banda de confianza superior para determinar si la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es menor que el límite superior. Si la banda de confianza superior es menor que el límite superior, usted puede afirmar que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es menor que el límite superior.
Diferencia: Media(Genérico) - Media(Marca)
| Diferencia | EE | Límite superior de 95% | Límite superior |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.21473 | 0.42503 |
En estos resultados, la banda de confianza superior de 95% para la diferencia es −0.21473, que es menor que el límite superior de −0.42503. Por lo tanto, usted puede estar 95% seguro de que la diferencia entre la media de la población de la prueba y la media de la población de referencia es menor que el límite superior.
Límite inferior
El límite de aceptabilidad inferior para la diferencia (o relación) entre la media de la prueba y la media de referencia. Usted desea que la diferencia (o relación) entre la media de la población de la muestra y la media de la población de referencia sea mayor que el límite inferior.
Interpretación
Compare el límite inferior con la banda de confianza inferior.Si la banda de confianza inferior es mayor que el límite inferior, usted puede afirmar que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es mayor el límite inferior.
Diferencia: Media(Genérico) - Media(Marca)
| Diferencia | EE | Límite inferior de 95% | Límite inferior |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.42735 | -0.42503 |
En estos resultados, la banda de confianza inferior de 95% para la diferencia es −0.42735, que es menor que el límite inferior de −0.42503. Por lo tanto, usted no puede afirmar que la diferencia entre la media de la población de la prueba y la media de la población de referencia es mayor que el límite inferior.
Límite superior
El límite de aceptabilidad superior para la diferencia (o relación) entre la media de la prueba y la media de referencia. Usted desea que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia sea menor que el límite superior.
Interpretación
Compare el límite superior con la banda de confianza superior. Si la banda de confianza superior es menor que el límite superior, usted puede afirmar que la diferencia (o relación) entre la media de la población de la prueba y la media de la población de referencia es menor que el límite superior.
Diferencia: Media(Genérico) - Media(Marca)
| Diferencia | EE | Límite superior de 95% | Límite superior |
|---|---|---|---|
| -0.32104 | 0.060641 | -0.21473 | 0.42503 |
En estos resultados, la banda de confianza superior de 95% para la diferencia es −0.21473, que es menor que el límite superior de −0.42503. Por lo tanto, usted puede estar 95% seguro de que la diferencia entre la media de la población de la prueba y la media de la población de referencia es menor que el límite superior.
