Un ingeniero en alimentos de una compañía de alimentos para mascotas somete a prueba una formulación nueva y menos costosa de la reconocida comida para gatos que produce la empresa. El ingeniero desea cerciorarse de que el contenido de proteínas de la formulación menos costosa sea igual al contenido proteínico de la formulación original. El ingeniero mide la cantidad de proteínas en muestras de 100 gramos de ambas formulaciones del alimento para determinar si son equivalentes con un margen de ±0.5 gramos.
El ingeniero realiza una prueba de equivalencia de 2 muestras para determinar si la diferencia media de proteínas entre las dos formulaciones está dentro de ±0.5 g. El ingeniero no sabe si las varianzas del contenido de proteínas son iguales para las dos formulaciones.
- Abra los datos de muestra, ProteínasAlimGatos.MWX.
- Elija .
- En la lista desplegable, seleccione Muestras en diferentes columnas.
- En Muestra para prueba, ingrese Descuento.
- En Muestra de referencia, ingrese Original.
- En Hipótesis sobre, seleccione Media de prueba - media de referencia.
- En ¿Qué desea deteminar? (hipótesis alterna), seleccione Límite inferior < media de prueba - media de referencia < límite superior.
- En Límite inferior, ingrese –0.5.
- En Límite superior, ingrese 0.5.
- Haga clic en Aceptar.
Interpretar los resultados
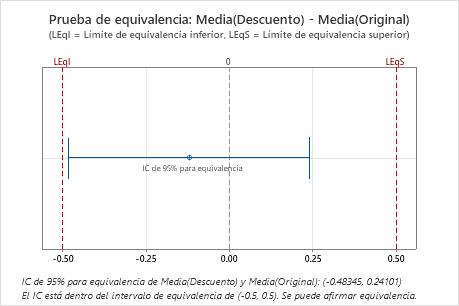
Puesto que el intervalo de confianza está completamente dentro del intervalo de equivalencia, el ingeniero concluye que las dos formulaciones de alimento para gatos contienen cantidades equivalentes de proteína.
Método
Media de referencia = media de Original
No se presupuso igualdad de varianzas para el análisis.
Estadísticas descriptivas
| Variable | N | Media | Desv.Est. | Error estándar de la media |
|---|---|---|---|---|
| Descuento | 10 | 33.971 | 0.58064 | 0.18361 |
| Original | 9 | 34.092 | 0.26138 | 0.087127 |
Diferencia: Media(Descuento) - Media(Original)
| Diferencia | EE | IC de 95% para equivalencia | Intervalo de equivalencia |
|---|---|---|---|
| -0.12122 | 0.20324 | (-0.483449, 0.241005) | (-0.5, 0.5) |
Prueba
| Hipótesis nula: | Diferencia ≤ -0.5 o Diferencia ≥ 0.5 |
|---|---|
| Hipótesis alterna: | -0.5 < Diferencia < 0.5 |
| Nivel de significancia: | 0.05 |
| Hipótesis nula | GL | Valor T | Valor p |
|---|---|---|---|
| Diferencia ≤ -0.5 | 12 | 1.8637 | 0.044 |
| Diferencia ≥ 0.5 | 12 | -3.0566 | 0.005 |