El valor Z es un estadístico de prueba para las pruebas Z que mide la diferencia entre un estadístico observado y su parámetro hipotético de población en unidades de la desviación estándar. Por ejemplo, un conjunto de moldes de fábrica tiene una profundidad media de 10 cm y una desviación estándar de 1 cm. Un molde con una profundidad de 12 cm tiene un valor Z de 2, porque su profundidad es dos desviaciones estándar mayor que la media. La línea vertical representa esta observación y su ubicación con respecto a toda la población:
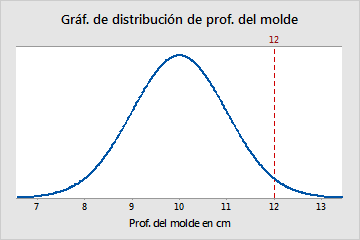
La conversión de una observación a un valor Z se denomina estandarización. Para estandarizar una observación de una población, reste la media de población a la observación de interés y divida el resultado entre la desviación estándar de la población. El resultado de estos cálculos es el valor Z asociado con la observación de interés.
Puede utilizar el valor Z para determinar si puede rechazar la hipótesis nula. Para determinar si puede rechazar la hipótesis nula, compare el valor Z con su valor crítico, que se puede encontrar en una tabla normal estándar en la mayoría de los libros de estadística. El valor crítico es Z1-α/2 para una prueba bilateral y Z1-α para una prueba unilateral. Si el valor absoluto del valor Z es mayor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula.
Por ejemplo, usted desea saber si un segundo grupo de moldes también tiene una profundidad media de 10 cm. Usted mide la profundidad de cada molde en el segundo grupo y calcula la profundidad media del grupo. Una prueba Z de 1 muestra calcula un valor Z de −1.03. Usted elige un nivel de significancia (α) de 0.05, lo que da como resultado un valor crítico de 1.96. Puesto que el valor absoluto del valor Z es menor que 1.96, usted no puede rechazar la hipótesis nula y no puede concluir que la profundidad media de los moldes es diferente de 10 cm.
