Los grados de libertad (GL) son la cantidad de información suministrada por los datos que usted puede "gastar" para estimar los valores de parámetros de población desconocidos y calcular la variabilidad de esas estimaciones. Este valor se determina según el número de observaciones de la muestra y el número de parámetros del modelo.
Si incrementa el tamaño de la muestra, obtendrá más información sobre la población y, por consiguiente, los grados de libertad de los datos aumentarán. Si agrega parámetros al modelo (por ejemplo, aumentando el número de términos en una ecuación de regresión), "gastará" información de los datos y reducirá los grados de libertad disponibles para estimar la variabilidad de las estimaciones de parámetros.
Los grados de libertad también se utilizan para caracterizar una distribución específica. Muchas familias de distribuciones, como t, F o chi-cuadrada, utilizan los grados de libertad para especificar cuál distribución t, F o chi-cuadrada específica es apropiada para diferentes tamaños de muestra y diferentes números de parámetros del modelo. Por ejemplo, la siguiente figura muestra las diferencias entre distribuciones de chi-cuadrada con diferentes grados de libertad.
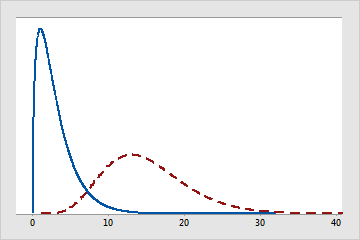
Distribuciones de chi-cuadrada con diferentes grados de libertad
La distribución de la línea de trazo continuo tiene 3 grados de libertad. La distribución de la línea de trazo interrumpido tiene 15 grados de libertad.
Ejemplos
Por ejemplo, la prueba t de 1 muestra solo estima un parámetro: la media de la población. El tamaño de la muestra de n constituye n informaciones para estimar la media de la población y su variabilidad. Un grado de libertad se gasta al estimar la media y los n-1 grados de libertad restantes estiman la variabilidad. Por lo tanto, un prueba t de 1 muestra utiliza una distribución t con n-1 grados de libertad.
Por el contrario, la regresión lineal múltiple debe estimar un parámetro para cada término que usted decida incluir en el modelo, y cada uno consume un grado de libertad. Por lo tanto, si se incluye un número excesivo de términos en un modelo de regresión lineal múltiple, se reducen los grados de libertad disponibles para estimar las variabilidad de los parámetros y la misma puede ser menos fiable.
