Un intervalo de confianza es un rango de valores, derivado de los estadísticos de la muestra, que posiblemente incluya el valor de un parámetro de población desconocido. Debido a su naturaleza aleatoria, es poco probable que dos muestras de una población en particular produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces su muestra, un determinado porcentaje de los intervalos de confianza resultantes incluiría el parámetro de población desconocido.
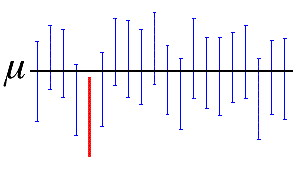
En este caso, la línea negra horizontal representa el valor fijo de la media desconocida de la población, µ. Los intervalos de confianza azules verticales que se sobreponen a la línea horizontal contienen el valor de la media de la población. El intervalo de confianza rojo que está completamente por debajo de la línea horizontal no lo contiene. Un intervalo de confianza de 95% indica que 19 de 20 muestras (95%) de la misma población producirán intervalos de confianza que contendrán el parámetro de población.
Utilice el intervalo de confianza para evaluar la estimación del parámetro de población. Por ejemplo, un fabricante desea saber si la longitud media de los lápices que produce es diferente de la longitud objetivo. El fabricante toma una muestra aleatoria de lápices y determina que la longitud media de la muestra es 52 milímetros y el intervalo de confianza de 95% es (50,54). Por lo tanto, usted puede estar 95% seguro de que la longitud media de todos los lápices se encuentra entre 50 y 54 milímetros.
- Estimación de punto
- Este valor individual estima un parámetro de población usando los datos de la muestra.
- Margen de error
-
Cuando usted utiliza estadísticos para estimar un valor, es importante recordar que, sin importar lo bien que esté diseñado su estudio, su estimación está sujeta a error de muestreo aleatorio. El margen de error cuantifica este error e indica la precisión de la estimación.
Usted probablemente ya entiende el margen de error, porque está relacionado con los resultados de las encuestas. Por ejemplo, una encuesta política podría indicar que el nivel de popularidad de un candidato es de 55% con un margen de error de 5%. Esto significa que el nivel de popularidad real es +/- 5% y, por lo tanto, se ubica entre 50% y 60%.
Para un intervalo de confianza bilateral, el margen de error es la distancia desde el estadístico estimado hasta cada el valor del intervalo de confianza. Cuando un intervalo de confianza es simétrico, el margen de error es la mitad del ancho del intervalo de confianza. Por ejemplo, la longitud media estimada de un árbol de levas es 600 mm y el intervalo de confianza oscila entre 599 y 601. El margen de error es 1.
Mientras mayor sea el margen de error, más ancho será el intervalo y menos seguro podrá estar usted del valor de la estimación de punto.
