Cuando se evalúa la relación entres dos variables, es importante determinar cómo se relacionan las variables. Las relaciones lineales son muy comunes, pero las variables también pueden tener una relación no lineal o monótona, como se muestra a continuación. También es posible que no haya relación entre las variables. Usted debería comenzar por crear una gráfica de dispersión de las variables para evaluar la relación.
Una relación lineal es una tendencia en los datos que se puede modelar mediante una línea recta. Por ejemplo, supongamos que una aerolínea desea estimar el impacto de los precios del combustible en los costos de los vuelos. Descubren que por cada dólar de aumento en el precio de un galón de combustible para aviones, el costo de su vuelo Los Angeles-Nueva York aumenta en aproximadamente $3500. Esto describe una relación lineal entre el costo del combustible para aviones y el costo del vuelo.
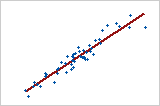
Gráfica 1: Relación lineal positiva fuerte
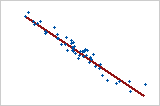
Gráfica 2: Relación lineal negativa fuerte
Cuando ambas variables aumentan o disminuyen simultáneamente a un ritmo constante, existe una relación lineal positiva. Los puntos de la Gráfica 1 siguen la línea muy de cerca, lo que sugiere que la relación entre las variables es fuerte. El coeficiente de correlación de Pearson para esta relación es +0.921.
Cuando una variable aumenta mientras la otra variable disminuye, existe una relación lineal negativa. Los puntos de la Gráfica 2 siguen la línea muy de cerca, lo que sugiere que la relación entre las variables es fuerte. El coeficiente de correlación de Pearson para esta relación es −0.968.
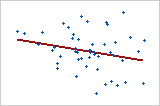
Gráfica 3: Relación lineal débil
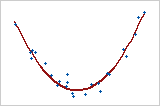
Gráfica 4: Relación no lineal
Los puntos de los datos de la Gráfica 3 parecen estar distribuidos de manera aleatoria. No se encuentran cerca de la línea, lo que indica una relación muy débil, si existe alguna. El coeficiente de correlación de Pearson para esta relación es −0.253.
Si una relación entre dos variables no es lineal, la tasa de aumento o descenso puede cambiar a medida que una variable cambia, causando un "patrón de curva" en los datos. Esta tendencia en forma de curva se podría modelar mejor mediante una función no lineal, como una función cuadrática o cúbica, o se podría transformar para convertirla en lineal. La Gráfica 4 muestra una relación fuerte entre dos variables. Sin embargo, puesto que la relación es no lineal, el coeficiente de correlación de Pearson es solo +0.244. Esta relación ilustra por qué es importante graficar los datos para poder explorar las relaciones que pudieran existir.
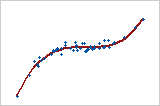
Gráfica 5: Relación monótona
En una relación monótona, las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante. En una relación lineal, las variables se mueven en la misma dirección a un ritmo constante. La Gráfica 5 revela que ambas variables aumentan al mismo tiempo, pero no al mismo ritmo. Esta relación es monótona, pero no lineal. El coeficiente de correlación de Pearson para estos datos es 0.843, pero la correlación de Spearman es mayor, 0.948.
Las relaciones lineales también son monótonas. Por ejemplo, la relación que se muestra en la Gráfica 1 es tanto monótona como lineal.
