En este tema
Media
Una medida frecuentemente utilizada del centro de un lote de números. La media también se denomina promedio. Es la suma de todas las observaciones dividida entre el número de observaciones (presentes).
Fórmula
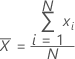
Notación
| Término | Description |
|---|---|
| xi | i ésima observación |
| N | número de observaciones presentes |
Error estándar de la media (EE de la media)
El error estándar de la media se calcula como la desviación estándar dividida entre la raíz cuadrada del tamaño de la muestra.
Fórmula

Notación
| Término | Description |
|---|---|
| s | desviación estándar de la muestra |
| N | número de observaciones presentes |
Desviación estándar (Desv.Est.)
La desviación estándar de la muestra proporciona una medida de la dispersión de los datos. Es igual a la raíz cuadrada de la varianza de la muestra.
Fórmula
 , entonces la desviación estándar de la muestra es:
, entonces la desviación estándar de la muestra es:
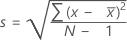
Notación
| Término | Description |
|---|---|
| x i | i ésima observación |
 | media de las observaciones |
| N | número de observaciones presentes |
Varianza
La varianza mide qué tan dispersos están los datos alrededor de su media. La varianza es igual a la desviación estándar elevada al cuadrado.
Fórmula
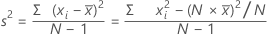
Notación
| Término | Description |
|---|---|
| xi | iésima observación |
 | media de las observaciones |
| N | número de observaciones presentes |
Coeficiente de variación (CoefVar)
El coeficiente de variación es una medida de la variabilidad relativa calculada como un porcentaje.
Fórmula

Minitab lo calcula como:

Notación
| Término | Description |
|---|---|
| s | desviación estándar de la muestra |
 | media de las observaciones |
1er cuartil (Q1)
25% de las observaciones de la muestra son menores que o iguales al valor del 1er cuartil. Por lo tanto, el 1er cuartil también se conoce como el percentil 25.
Fórmula

Notación
| Término | Description |
|---|---|
| Y | valor entero truncado de w |
| w | 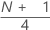 |
| z | componente fraccionado de w que fue truncado |
| xj | jiésima observación en la lista de datos de la muestra, ordenados del más pequeño al más grande |
Nota
Cuando w es un entero, y = w, z = 0 y Q1 = xy.
Mediana
La mediana de la muestra está en la mitad de los datos: por lo menos la mitad de las observaciones es menor que o igual a la mediana y por lo menos la mitad de las observaciones es mayor que o igual a la mediana.
Supongamos que usted tiene una columna que contiene N valores. Para calcular la mediana, primero ordene los valores de los datos del más pequeño al más grande. Si N es impar, la mediana de la muestra es el valor del medio. Si N es par, la mediana es el promedio de los dos valores del medio.
Por ejemplo, cuando N = 5 y usted tiene los datos x1, x2, x3, x4 y x5, la mediana = x3.
Cuando N = 6 y usted ordenó los datos x1, x2, x3, x4, x5 y x6:

donde x3 y x4 son la tercera y la cuarta observación
3er cuartil (Q3)
75% de las observaciones de la muestra son menores que o iguales al valor del tercer cuartil. Por lo tanto, el tercer cuartil también se conoce como el percentil 75.
Fórmula

Notación
| Término | Description |
|---|---|
| Y | valor truncado de w |
| w |
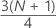 |
| z | componente fraccionado de w que fue truncado |
| xj | jiésima observación en la lista de datos de la muestra, ordenados del más pequeño al más grande |
Nota
Cuando w es un entero, y = w, z = 0 y Q3 = xy.
Rango intercuartil (IQR)
El rango intercuartil es igual al tercer cuartil menos el 1er cuartil.
Media recortada (MediaRec)
Minitab calcula la media recortada eliminando el 5% más pequeño y el 5% más grande de los valores (redondeados al entero más cercano) y calculando luego la media de los valores restantes.
Suma
Fórmula

Notación
| Término | Description |
|---|---|
| xi | i ésima observación |
Mínimo
El valor más pequeño del conjunto de datos.
Máximo
El valor más grande del conjunto de datos.
Rango
El rango se calcula como la diferencia entre el valor más grande y el valor más pequeño de los datos.
R = Máximo – Mínimo
Suma de los cuadrados
Minitab eleva al cuadrado cada uno de los valores de la columna y luego calcula la suma de esos valores elevados al cuadrado.
Fórmula
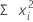
Notación
| Término | Description |
|---|---|
| xi | i ésima observación |
Asimetría
La asimetría es una medida de la condición asimétrica. Un valor negativo indica asimetría a la izquierda y un valor positivo indica asimetría a la derecha. Un valor de cero no necesariamente indica simetría.
Fórmula
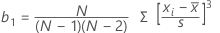
Notación
| Término | Description |
|---|---|
| xi | i ésima observación |
 | media de las observaciones |
| N | número de observaciones presentes |
| s | desviación estándar de la muestra |
Curtosis
La curtosis es una medida de qué tan diferente es una distribución con respecto a la distribución normal. Un valor positivo por lo general indica que la distribución tiene un pico más pronunciado que la distribución normal. Un valor negativo indica que la distribución tiene un pico más plano que la distribución normal.
Fórmula

Notación
| Término | Description |
|---|---|
| xi | i ésima observación |
 | media de las observaciones |
| N | número de observaciones presentes |
| s | desviación estándar de la muestra |
MSSD (media de las diferencias sucesivas cuadráticas)
Minitab calcula la mitad de la MSSD (media de las diferencias sucesivas cuadráticas) de un lote de números. Las diferencias sucesivas se elevan al cuadrado y se suman. Después, Minitab divide entre 2 y calcula el promedio.
Fórmula
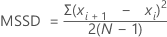
Notación
| Término | Description |
|---|---|
| xi | i ésima observación |
 | media de las observaciones |
N valores presentes (N)
El número de valores presentes en la muestra.
N valores faltantes (N*)
El número de valores faltantes en la muestra. El número de valores faltantes se refiere a las celdas que contienen el símbolo de valor faltante *.
N total (conteo total)
El número total de observaciones en la columna.
Porcentaje
Minitab calcula qué porcentaje del total corresponde a cada grupo.
Fórmula

Notación
| Término | Description |
|---|---|
| ni | número de observaciones en el iésimo grupo |
| N | número de observaciones presentes |
Porcentaje acumulado (PctAcum)
Minitab calcula el porcentaje acumulado que representa cada grupo.
Fórmula
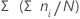
Notación
| Término | Description |
|---|---|
| ni | número de observaciones en el iésimo grupo |
| N | número de observaciones presentes |
