En este tema
Media
La media es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
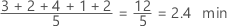
Interpretación
Utilice la media para describir la muestra con un solo valor que representa el centro de los datos. Muchos análisis estadísticos utilizan la media como una medida estándar del centro de la distribución de los datos.
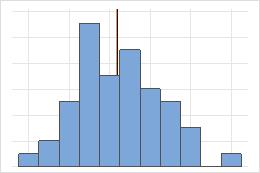
Simétrica
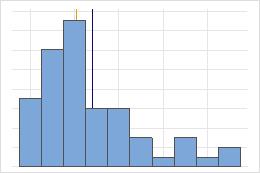
No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
EE de la media
El error estándar de la media (EE de la media) estima la variabilidad entre las medias de las muestras que usted obtendría si tomara muestras repetidas de la misma población. Mientras que el error estándar de la media estima la variabilidad entre las muestras, la desviación estándar mide la variabilidad dentro de una misma muestra.
Por ejemplo, usted tiene un tiempo de entrega medio de 3.80 días, con una desviación estándar de 1.43 días, de una muestra aleatoria de 312 tiempos de entrega. Estos números producen un error estándar de la media de 0.08 días (1.43 dividido entre la raíz cuadrada de 312). De haber tomado múltiples muestras aleatorias del mismo tamaño y de la misma población, la desviación estándar de esas medias diferentes de las muestras habría sido aproximadamente 0.08 días.
Interpretación
Utilice el error estándar de la media para determinar el grado de precisión con el que la media de la muestra estima la media de la población.
Un valor del error estándar de la media más bajo indica una estimación más precisa de la media de la población. Por lo general, una desviación estándar más grande se traducirá en un mayor error estándar de la media y una estimación menos precisa de la media de la población. Un tamaño de muestra más grande dará como resultado un menor error estándar de la media y una estimación más precisa de la media de la población.
Minitab utiliza el error estándar de la media para calcular el intervalo de confianza.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
Debido a que la desviación estándar utiliza las mismas unidades que los datos, generalmente es más fácil de interpretar que la varianza.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersos están los datos con respecto a la media. Un valor de desviación estándar más alto indica una mayor dispersión de los datos. Una buena regla empírica para una distribución normal es que aproximadamente 68% de los valores se ubican dentro de una desviación estándar de la media, 95% de los valores se ubican dentro de dos desviaciones estándar y 99.7% de los valores se ubican dentro de tres desviaciones estándar.
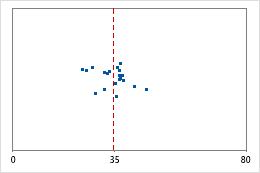
Hospital 1
Hospital 2
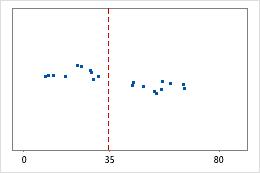
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Varianza
La varianza mide qué tan dispersos están los datos alrededor de su media. La varianza es igual a la desviación estándar elevada al cuadrado.
Interpretación
Mientras mayor sea la varianza, mayor será la dispersión de los datos.
Puesto que la varianza (σ2) es una cantidad elevada al cuadrado, sus unidades también están elevadas al cuadrado, lo que puede dificultar el uso de la varianza en la práctica. La desviación estándar generalmente es más fácil de interpretar porque utiliza las mismas unidades que los datos. Por ejemplo, una muestra del tiempo de espera en una parada de autobuses puede tener una media de 15 minutos y una varianza de 9 minutos2. Debido a que la varianza no está en las mismas unidades que los datos, la varianza suele mostrarse con su raíz cuadrada, la desviación estándar. Una varianza de 9 minutos2 es equivalente a una desviación estándar de 3 minutos.
CoefVar
El coeficiente de variación (denotado como COV) es una medida de dispersión que describe la variación en los datos en relación con la media. El coeficiente de variación se ajusta de manera que los valores estén en una escala sin unidades. Gracias a este ajuste, usted puede utilizar el coeficiente de variación en lugar de la desviación estándar para comparar la variación de los datos que tienen unidades diferentes o medias muy diferentes.
Interpretación
Mientras mayor sea el coeficiente de variación, mayor será la dispersión en los datos.
| Recipiente grande | Recipiente pequeño |
|---|---|
| COV = 100 * 0.4 tazas / 16 tazas = 2.5 | COV = 100 * 0.08 tazas / 1 taza = 8 |
Q1
Los cuartiles son los tres valores –el primer cuartil en 25% (Q1), el segundo cuartil en 50% (Q2 o mediana) y el tercer cuartil en 75% (Q3)– que dividen una muestra de datos ordenados en cuatro partes iguales.
El primer cuartil es el percentil 25 e indica que 25% de los datos es menor que o igual a este valor.
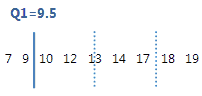
Para estos datos ordenados, el primer cuartil (Q1) es 9.5. Es decir, 25% de los datos es menor que o igual a 9.5.
Mediana
La mediana es el punto medio del conjunto de datos. El valor de este punto medio es el punto en el cual la mitad de las observaciones está por encima del valor y la otra mitad está por debajo del valor. La mediana se determina jerarquizando las observaciones y hallando la observación que ocupe el número [N + 1] / 2 en el orden jerarquizado. Si el número de observaciones es par, entonces la mediana es el valor promedio de las observaciones jerarquizadas en los números N / 2 y [N / 2] + 1.
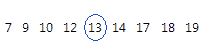
Para estos datos ordenados, la mediana es 13. Es decir, la mitad de los valores es menor que o igual a 13 y la otra mitad de los valores es mayor que o igual a 13. Si usted agrega otra observación igual a 20, la mediana es 13,5, que es el promedio entre la 5ta observación (13) y la 6ta observación (14).
Interpretación

Simétrica

No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
Q3
Los cuartiles son los tres valores –el primer cuartil en 25% (Q1), el segundo cuartil en 50% (Q2 o mediana) y el tercer cuartil en 75% (Q3)– que dividen una muestra de datos ordenados en cuatro partes iguales.
El tercer cuartil es el percentil 75 e indica que 75% de los datos es menor que o igual a este valor.
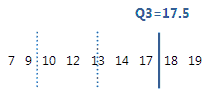
Para estos datos ordenados, el tercer cuartil (Q3) es 17.5. Es decir, 75% de los datos es menor que o igual a 17.5.
IQR
El rango intercuartil (IQR) es la distancia entre el primer cuartil (Q1) y el tercer cuartil (Q3). El 50% de los datos está dentro de este rango.
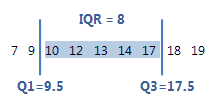
Para estos datos ordenados, el rango intercuartil es 8 (17.5–9.5 = 8). Es decir, el 50% intermedio de los datos está entre 9.5 and 17.5.
Interpretación
Utilice el rango intercuartil para describir la dispersión de los datos. A medida que aumenta la dispersión de los datos, el IQR se hace más grande.
MediaRec
La media de los datos sin el 5% superior ni el 5% inferior de los valores.
Utilice la media recortada para eliminar el impacto de los valores muy grandes o muy pequeños sobre la media. Cuando los datos contienen valores atípicos, la media recortada puede ser una mejor medida de la tendencia central que la media.
Suma
La suma es el total de todos los valores de los datos. La suma también se utiliza en cálculos estadísticos, como por ejemplo la media y la desviación estándar.
Mínimo
El mínimo es el valor más pequeño de los datos.
En estos datos, el mínimo es 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el mínimo para identificar un posible valor atípico o un error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor mínimo es muy bajo, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Máximo
El máximo es el valor más grande de los datos.
En estos datos, el máximo es 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el máximo para identificar un posible valor atípico o error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor máximo es muy alto, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Rango
El rango es la diferencia entre los valores más grande y más pequeño de los datos. El rango representa el intervalo que contiene todos los valores de los datos.
Interpretación
Utilice el rango para entender la cantidad de dispersión en los datos. Un valor de rango grande indica mayor dispesión en los datos. Un valor de rango pequeño indica que hay menos dispersión en los datos. Puesto que el rango se calcula usando solo dos valores de los datos, es más útil con conjuntos de datos pequeños.
SSQ
La suma de los cuadrados no corregida es la suma de los cuadrados de cada valor de la columna. Por ejemplo, si la columna contiene x1, x2, ... , xn, entonces la suma de los cuadrados calcula (x12 + x22 + ... + xn2). A diferencia de la suma de los cuadrados corregida, la suma de los cuadrados no corregida incluye el error. Los valores de datos se elevan al cuadrado sin antes restar la media.
Asimetría
La asimetría es el grado en que los datos no son simétricos.
Interpretación
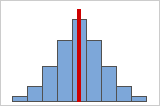
Figura A
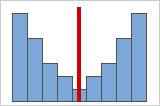
Figura B
Distribuciones simétricas o no asimétricas
A medida que los datos se vuelven más simétricos, el valor de su asimetría se acerca a cero. La figura A muestra datos distribuidos normalmente, que por definición exhiben relativamente poca asimetría. Al dibujar una línea por debajo de la mitad de este histograma de datos normales, se puede ver fácilmente que un lado es el reflejo del otro. Pero la falta de asimetría por sí sola no implica normalidad. La figura B muestra una distribución en la que ambos lados siguen siendo un reflejo el uno del otro, a pesar de que la distribución de los datos dista mucho de ser normal.
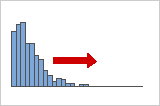
Distribuciones asimétricas positivas o hacia la derecha
Los datos con asimetría positiva o asimétricos hacia la derecha se llaman así porque la "cola" de la distribución apunta hacia la derecha y porque el valor de asimetría es mayor que 0 (es decir, positivo). Los datos sobre salarios suelen ser asimétricos de esta manera: muchos empleados de una empresa ganan relativamente poco, mientras que cada vez menos personas ganan salarios muy elevados.
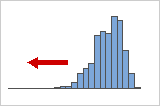
Distribuciones asimétricas negativas o hacia la izquierda
Los datos asimétricos hacia la izquierda o con asimetría negativa se llaman así porque la "cola" de la distribución apunta hacia la izquierda y porque producen un valor de asimetría negativo. Los datos de tasas de fallas suelen ser asimétricos a la izquierda. Consideremos el caso de las bombillas: muy pocas se quemarán inmediatamente, la gran mayoría dura un tiempo considerablemente largo.
Curtosis
La curtosis indica la manera en que las colas de una distribución difieren de la distribución normal.
Interpretación
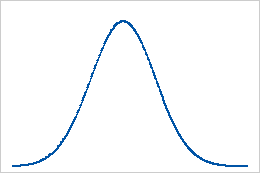
Línea de base: Valor de curtosis de 0
Los datos normalmente distribuidos establecen la línea de base para la curtosis. Un valor de curtosis de 0 indica que los datos siguen perfectamente la distribución normal. Un valor de curtosis que se desvía significativamente de 0 puede indicar que los datos no están distribuidos normalmente.
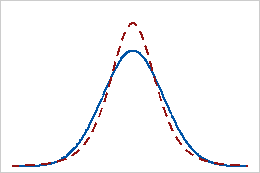
Curtosis positiva
Una distribución que tiene un valor positivo de curtosis indica que la distribución tiene colas más pesadas que la distribución normal. Por ejemplo, los datos que siguen una distribución t tienen un valor positivo de curtosis. La línea continua indica la distribución normal y la línea de puntos indica una distribución que tiene un valor positivo de curtosis.
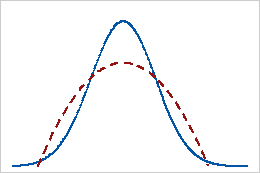
Curtosis negativa
Una distribución con un valor negativo de curtosis indica que la distribución tiene colas más livianas que la distribución normal. Por ejemplo, los datos que siguen una distribución beta con el primer y el segundo parámetro de forma iguales a 2 tienen un valor negativo de curtosis. La línea continua indica la distribución normal y la línea de puntos indica una distribución que tiene un valor negativo de curtosis.
MSSD
La MSSD es la media de las diferencias sucesivas cuadráticas. La MSSD es una estimación de la varianza. Un posible uso de la MSSD es para probar si una secuencia de observaciones es aleatoria. En control de calidad, un posible uso de la MSSD es para estimar la varianza cuando el tamaño del subgrupo = 1.
N
El número de valores presentes en la muestra.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N valores faltantes
El número de valores faltantes en la muestra. El número de valores faltantes se refiere a las celdas que contienen el símbolo de valor faltante *.
| Conteo total | N | N valores faltantes |
|---|---|---|
| 149 | 141 | 8 |
Conteo
El número total de observaciones en la columna. Utilícese para representar la suma de N valores faltantes y N valores presentes.
| Conteo | N | N valores faltantes |
|---|---|---|
| 149 | 141 | 8 |
NAcum
| Nivel de grado | Conteo | NAcum | Cálculo |
|---|---|---|---|
| 1 | 49 | 49 | 49 |
| 2 | 58 | 107 | 49 + 58 |
| 3 | 52 | 159 | 49 + 58 + 52 |
| 4 | 60 | 219 | 49 + 58 + 52 + 60 |
| 5 | 48 | 267 | 49 + 58 + 52 + 60 + 48 |
| 6 | 55 | 322 | 49 + 58 + 52 + 60 + 48 + 55 |
Porcentaje
El porcentaje de observaciones en cada grupo de la Por variable. En el siguiente ejemplo, hay cuatro grupos: Línea 1, Línea 2, Línea 3 y Línea 4.
| Grupo (por variable) | Porcentaje |
|---|---|
| Línea 1 | 16 |
| Línea 2 | 20 |
| Línea 3 | 36 |
| Línea 4 | 28 |
PAcum
El porcentaje acumulado es la suma acumulada de los porcentajes para cada grupo de la Por variable. En el siguiente ejemplo, la Por variable tiene 4 grupos: Línea 1, Línea 2, Línea 3 y Línea 4.
| Grupo (por variable) | Porcentaje | PAcum |
|---|---|---|
| Línea 1 | 16 | 16 |
| Línea 2 | 20 | 36 |
| Línea 3 | 36 | 72 |
| Línea 4 | 28 | 100 |
