En este tema
N
El tamaño de la muestra (N) es el número total de observaciones en la muestra.
Interpretación
El tamaño de la muestra afecta el intervalo de confianza y la potencia de la prueba.
Generalmente, un tamaño de la muestra más grande da como resultado un intervalo de confianza más estrecho. Con un tamaño de la muestra más grande, la prueba también tendrá más potencia para detectar una diferencia. Para obtener más información, vaya a ¿Qué es potencia?.
Media
Minitab presenta la media de cada muestra y la media de las diferencias entre las observaciones pareadas.
La media resume los valores de la muestra con un valor individual que representa el centro de los datos. La media es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
Interpretación
La diferencia en las medias es una estimación de la diferencia en las medias de las poblaciones.
Puesto que la diferencia en las medias se basa en los datos de una muestra y no en toda la población, es improbable que la diferencia en las medias de las muestras sea igual a la diferencia en las medias de las poblaciones. Para estimar mejor la diferencia en las medias de las poblaciones, utilice el intervalo de confianza de la diferencia.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
La desviación estándar utiliza las mismas unidades que los datos.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersos están los datos con respecto a la media. Un valor de desviación estándar más alto indica una mayor dispersión de los datos. Una buena regla empírica para una distribución normal es que aproximadamente 68% de los valores se ubican dentro de una desviación estándar de la media, 95% de los valores se ubican dentro de dos desviaciones estándar y 99.7% de los valores se ubican dentro de tres desviaciones estándar.
La desviación estándar de los datos de la muestra es una estimación de la desviación estándar de la población. La desviación estándar se usa para calcular el intervalo de confianza y el valor p. Un valor más alto produce intervalos de confianza menos precisos (más amplios) y pruebas menos potentes.
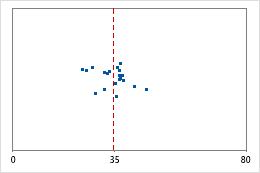
Hospital 1
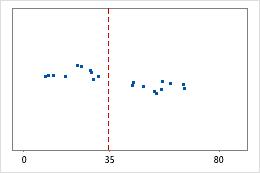
Hospital 2
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
EE de la media
El error estándar de la media (EE de la media) estima la variabilidad entre las medias de las muestras que usted obtendría si tomara muestras repetidas de la misma población. Mientras que el error estándar de la media estima la variabilidad entre las muestras, la desviación estándar mide la variabilidad dentro de una misma muestra.
Por ejemplo, usted tiene un tiempo de entrega medio de 3.80 días, con una desviación estándar de 1.43 días, de una muestra aleatoria de 312 tiempos de entrega. Estos números producen un error estándar de la media de 0.08 días (1.43 dividido entre la raíz cuadrada de 312). De haber tomado múltiples muestras aleatorias del mismo tamaño y de la misma población, la desviación estándar de esas medias diferentes de las muestras habría sido aproximadamente 0.08 días.
Interpretación
Utilice el error estándar de la media para determinar el grado de precisión con el que la media de la muestra estima la media de la población.
Un valor del error estándar de la media más bajo indica una estimación más precisa de la media de la población. Por lo general, una desviación estándar más grande se traducirá en un mayor error estándar de la media y una estimación menos precisa de la media de la población. Un tamaño de muestra más grande dará como resultado un menor error estándar de la media y una estimación más precisa de la media de la población.
Minitab utiliza el error estándar de la media para calcular el intervalo de confianza.
Intervalo de confianza (IC) y límites
El intervalo de confianza proporciona un rango de valores probables para la diferencia en las medias de las poblaciones. Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces la muestra, un determinado porcentaje de los intervalos o bordes de confianza resultantes contendría la diferencia desconocida en las medias de las poblaciones. El porcentaje de estos intervalos o bordes de confianza que contiene la diferencia en las medias es el nivel de confianza del intervalo. Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan la diferencia en las medias de las poblaciones.
Un borde superior define un valor en comparación con el cual es probable que la diferencia en las medias de las poblaciones sea menor. Un borde inferior define un valor en comparación con el cual es probable que la diferencia en las medias de las poblaciones sea mayor.
El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra. Para obtener más información, vaya a Maneras de obtener un intervalo de confianza más preciso.
Estimación de la diferencia pareada
| Media | Desv.Est. | Error estándar de la media | IC de 95% para la diferencia_µ |
|---|---|---|---|
| 2.200 | 3.254 | 0.728 | (0.677, 3.723) |
En estos resultados, la estimación de la diferencia en las medias de las poblaciones para el ritmo cardíaco es 2,2. Usted puede estar 95% seguro de que la diferencia en las medias de las poblaciones está entre 0,677 y 3,723.
Hipótesis nula e hipótesis alternativa
- Hipótesis nula
- La hipótesis nula indica que un parámetro de población (tal como la media, la desviación estándar, etc.) es igual a un valor hipotético. La hipótesis nula suele ser una afirmación inicial que se basa en análisis previos o en conocimiento especializado.
- Hipótesis alternativa
- La hipótesis alternativa establece que un parámetro de población es más pequeño, más grande o diferente del valor hipotético de la hipótesis nula. La hipótesis alternativa es lo que usted podría pensar que es cierto o espera probar que es cierto.
En la salida, las hipótesis nula y alternativa le ayudan a verificar que usted ingresó el valor correcto de la diferencia de la prueba.
Valor t
El valor t es el valor observado del estadístico de la prueba t que mide la diferencia entre un estadístico de muestra observado y su parámetro hipotético de población en unidades de error estándar.
Interpretación
Usted puede comparar el valor t con los valores críticos de la distribución t para determinar si puede rechazar la hipótesis nula. Sin embargo, por lo general es más práctico y conveniente utilizar el valor p de la prueba para hacer la misma determinación.
Para determinar si puede rechazar la hipótesis nula, compare el valor t con el valor crítico. El valor crítico es tα/2, n–1 para una prueba bilateral y tα, n–1 para una prueba unilateral. Para una prueba bilateral, si el valor absoluto del valor t es mayor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula. Puede calcular el valor crítico en Minitab o buscar el valor crítico en una tabla de distribución t en la mayoría de los libros de estadística. Para obtener más información, vaya a Uso de la función de distribución acumulada inversa (ICDF) y haga clic en "Usar la ICDF para calcular los valores críticos".
Valor p
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si la media de las diferencias de las poblaciones es estadísticamente diferente de la media de las diferencias hipotética.
- Valor p ≤ α: La diferencia entre las medias es estadísticamente significativa (Rechazar H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula. Usted puede concluir que la diferencia entre las medias de las poblaciones no es igual a la diferencia hipotética. Si no especificó una diferencia hipotética, Minitab prueba si no hay diferencia entre las medias (Diferencia hipotetizada = 0) Utilice su conocimiento especializado para determinar si la diferencia es significativa desde el punto de vista práctico. Para obtener más información, vaya a Significancia estadística y práctica.
- Valor p > α: La diferencia entre las medias no es estadísticamente significativa (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que la diferencia en las medias entre las observaciones pareadas es estadísticamente significativa. Debe asegurarse de que su prueba tenga suficiente potencia para detectar una diferencia que es significativa desde el punto de vista práctico. Para obtener más información, vaya a Potencia y tamaño de la muestra para t pareada.
Histograma
Un histograma divide los valores de la muestra en muchos intervalos y representa la frecuencia de los valores de datos en cada intervalo con una barra.
Interpretación
Utilice un histograma para evaluar la forma y dispersión de los datos. Los histogramas funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
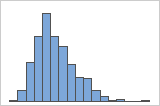
Asimétrico hacia la derecha
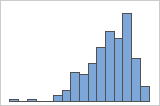
Asimétrico hacia la izquierda
El histograma con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. El histograma con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Los datos que son marcadamente asimétricos pueden afectar la validez del valor p si la muestra es pequeña (menos de 20 valores). Si los datos son marcadamente asimétricos y usted tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
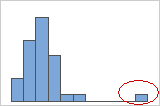
En un histograma, las barras aisladas en cualquiera de los extremos de la gráfica identifican posibles valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
Gráfica de valores individuales
Una gráfica de valores individuales muestra los valores individuales en la muestra. Cada círculo representa una observación. Una gráfica de valores individuales es especialmente útil cuando usted tiene relativamente pocas observaciones y cuando también necesita evaluar el efecto de cada observación.
Interpretación
Utilice una gráfica de valores individuales para examinar la dispersión de los datos y para identificar cualquier posible valor atípico. Las gráficas de valores individuales funcionan mejor cuando el tamaño de la muestra es menor que 50.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
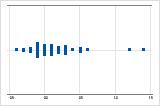
Asimétrico hacia la derecha
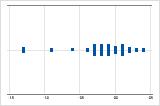
Asimétrico hacia la izquierda
La gráfica de valores individuales con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. La gráfica de valores individuales con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Los datos que son marcadamente asimétricos pueden afectar la validez del valor p si la muestra es pequeña (menos de 20 valores). Si los datos son marcadamente asimétricos y usted tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
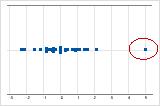
En una gráfica de valores individuales, los valores de datos extrañamente bajos o altos indican posibles valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
Gráfica de caja
Una gráfica de caja proporciona un resumen gráfico de la distribución de una muestra. La gráfica de caja muestra la forma, tendencia central y variabilidad de los datos.
Interpretación
Utilice una gráfica de caja para examinar la dispersión de los datos y para identificar cualquier posible valor atípico. Las gráficas de caja funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
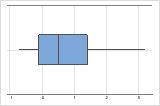
Asimétrico hacia la derecha
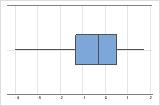
Asimétrico hacia la izquierda
La gráfica de caja con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. La gráfica de caja con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Los datos que son marcadamente asimétricos pueden afectar la validez del valor p si la muestra es pequeña (menos de 20 valores). Si los datos son marcadamente asimétricos y usted tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
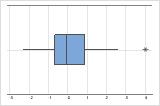
En una gráfica de caja, los asteriscos (*) denotan valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
