En este tema
Paso 1: Determinar si existe un valor atípico
- Valor p ≤ α: Existe un valor atípico (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que existe un valor atípico. Intente identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales).
- Valor p > α: Usted no puede concluir que existe un valor atípico (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula, porque no cuenta con suficiente evidencia para concluir que existe un valor atípico. Debe asegurarse de que su prueba tenga suficiente potencia para detectar un valor atípico. Para obtener más información, vaya a Aumentar la potencia.
Método
| Hipótesis nula | Todos los valores de los datos provienen de la misma población normal |
|---|---|
| Hipótesis alterna | El valor más pequeño de los datos es un valor atípico |
| Nivel de significancia | α = 0.05 |
Prueba de Grubbs
| Variable | N | Media | Desv.Est. | Mín. | Máx. | G | P |
|---|---|---|---|---|---|---|---|
| ResistRotura | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
Valor atípico
| Variable | Fila | Valor atípico |
|---|---|---|
| ResistRotura | 10 | 12.38 |
Resultado clave: P
En estos resultados, la hipótesis nula indica que todos los valores de los datos provienen de la misma población normal. Puesto que el valor p es 0.044, que es menor que el nivel de significancia de 0.05, la decisión es rechazar la hipótesis nula y concluir que existe un valor atípico.
Paso 2: Determinar el valor del valor atípico
Si la prueba identifica un valor atípico en los datos, entonces Minitab muestra una tabla de valores atípicos. Utilice la tabla de valores atípicos para determinar el valor del valor atípico y la fila de la hoja de trabajo que contiene el valor atípico.
Método
| Hipótesis nula | Todos los valores de los datos provienen de la misma población normal |
|---|---|
| Hipótesis alterna | El valor más pequeño de los datos es un valor atípico |
| Nivel de significancia | α = 0.05 |
Prueba de Grubbs
| Variable | N | Media | Desv.Est. | Mín. | Máx. | G | P |
|---|---|---|---|---|---|---|---|
| ResistRotura | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
Valor atípico
| Variable | Fila | Valor atípico |
|---|---|---|
| ResistRotura | 10 | 12.38 |
Resultados clave: Fila, valor atípico
En estos resultados, el valor del valor atípico es 12.38 y está en la fila 10.
Paso 3: Identificar visualmente el valor atípico
Utilice la gráfica de valores atípicos para identificar visualmente un valor atípico en los datos. Si existe un valor atípico, Minitab lo representa en la gráfica como un cuadro rojo. Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales).
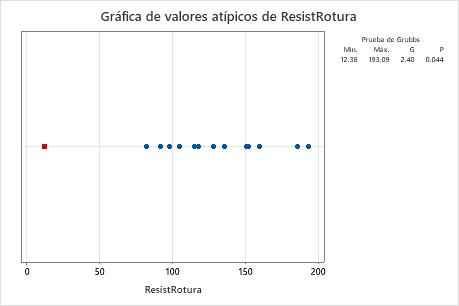
En esta gráfica de valores atípicos, el valor más pequeño, 12.38, es un valor atípico.
