En este tema
Hipótesis nula e hipótesis alternativa
- Hipótesis nula
- La hipótesis nula indica que todos los valores de los datos provienen de la misma distribución normal.
- Hipótesis alterna
- La hipótesis alternativa indica que el valor más pequeño o más grande de los datos es un valor atípico.
Nivel de significancia
El nivel de significancia (denotado como α o alfa) es el máximo nivel de riesgo aceptable de rechazar la hipótesis nula cuando la hipótesis nula es verdadera (error tipo I). El valor predeterminado es 0.05.
Interpretación
Utilice el nivel de significancia para decidir si rechaza o no rechaza la hipótesis nula (H0). Si la probabilidad de que ocurra un evento es menor que el nivel de significancia, la interpretación habitual es que los resultados son estadísticamente significativos y usted rechaza H0.
- Elija un nivel de significancia más alto, como por ejemplo 0.10, para estar más seguro de detectar cualquier diferencia que pueda existir. Por ejemplo, un ingeniero especializado en calidad compara la estabilidad de nuevos rodamientos de esferas con la estabilidad de los rodamientos actuales. El ingeniero debe estar sumamente seguro de que los nuevos rodamientos de esferas son estables, porque rodamientos inestables podrían causar un desastre. Escoge un nivel de significancia de 0.10 para estar más seguro de detectar cualquier posible diferencia en la estabilidad de los rodamientos.
- Elija un nivel de significancia más bajo, como por ejemplo 0.01, para estar más seguro de detectar solo una diferencia que realmente exista. Por ejemplo, un científico de una compañía farmacéutica debe estar muy seguro de que la afirmación de que el nuevo medicamento de la empresa reduce significativamente los síntomas es verdadera. El científico escoge un nivel de significancia de 0.001 para estar más seguro de que existe una diferencia significativa en los síntomas.
N
El tamaño de la muestra (N) es el número total de observaciones en la muestra.
Interpretación
El tamaño de la muestra afecta la potencia de la prueba.
Por lo general, con un tamaño de muestra más grande, la prueba tiene más potencia para detectar un valor atípico. Para obtener más información, vaya a ¿Qué es potencia?.
Media
La media es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
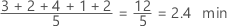
Interpretación
Utilice la media para describir la muestra con un solo valor que representa el centro de los datos. Muchos análisis estadísticos utilizan la media como una medida estándar del centro de la distribución de los datos.
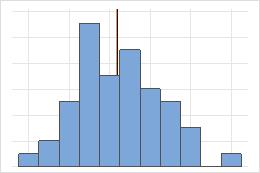
Simétrica
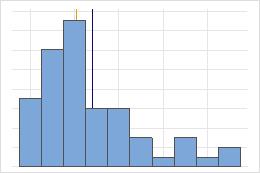
No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
Debido a que la desviación estándar utiliza las mismas unidades que los datos, generalmente es más fácil de interpretar que la varianza.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersos están los datos con respecto a la media. Un valor de desviación estándar más alto indica una mayor dispersión de los datos. Una buena regla empírica para una distribución normal es que aproximadamente 68% de los valores se ubican dentro de una desviación estándar de la media, 95% de los valores se ubican dentro de dos desviaciones estándar y 99.7% de los valores se ubican dentro de tres desviaciones estándar.
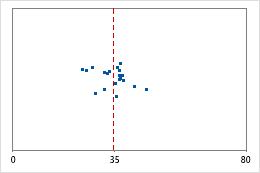
Hospital 1
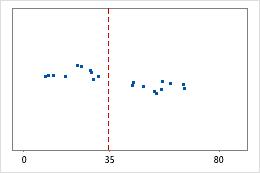
Hospital 2
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Máximo
El máximo es el valor más grande de los datos.
En estos datos, el máximo es 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el máximo para identificar un posible valor atípico o error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor máximo es muy alto, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Mínimo
El mínimo es el valor más pequeño de los datos.
En estos datos, el mínimo es 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el mínimo para identificar un posible valor atípico o un error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor mínimo es muy bajo, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Valor atípico
Un valor atípico es una observación extrañamente grande o pequeña. Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales).
Fila
La fila de la hoja de trabajo que contiene el valor atípico. Minitab solo muestra este valor cuando existe un valor atípico.
x[i] y x[N-i]
Cuando usted utiliza una de las pruebas de relación de Dixon, Minitab muestra más observaciones en la tabla de la prueba, además del mínimo y el máximo. El valor entre corchetes indica el tamaño de la observación con respecto a los otros valores. Por ejemplo, x[2] denota la 2da observación más pequeña y x[N-1] denota la 2da observación más grande.
G
El estadístico de la prueba de Grubbs (G) es la diferencia entre la media de la muestra y el valor de los datos más grande o más pequeño, dividida entre la desviación estándar. Minitab utiliza el estadístico de la prueba de Grubbs para calcular el valor p, que es la probabilidad de rechazar la hipótesis nula cuando es verdadera.
P
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si existe un valor atípico.
- Valor p ≤ α: Existe un valor atípico (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que existe un valor atípico. Intente identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales).
- Valor p > α: Usted no puede concluir que existe un valor atípico (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula, porque no cuenta con suficiente evidencia para concluir que existe un valor atípico. Debe asegurarse de que su prueba tenga suficiente potencia para detectar un valor atípico. Para obtener más información, vaya a Aumentar la potencia.
Gráfica de valores atípicos
Una gráfica de valores atípicos es similar a una gráfica de valores individuales. Utilice la gráfica de valores atípicos para identificar visualmente un valor atípico en los datos. Si existe un valor atípico, Minitab lo representa en la gráfica como un cuadro rojo. Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales).
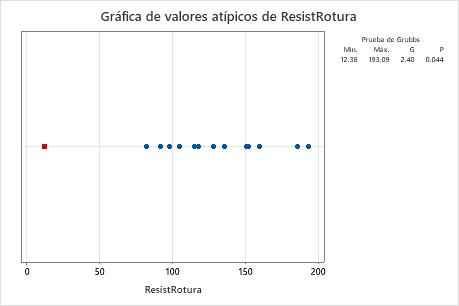
En estos resultados, el valor más pequeño, 12.38, es un valor atípico.
