Un ingeniero especializado en calidad que trabaja en una empresa que produce mangos de madera evalúa la resistencia de una muestra aleatoria de palos de escoba. El ingeniero registra la fuerza que se necesita para romper cada palo. El ingeniero crea una gráfica de los datos y se percata de que uno de los valores de la muestra parece extrañamente bajo.
El ingeniero realiza una prueba de valores atípicos para determinar si el valor más pequeño es un valor atípico.
- Abra los datos de muestra, ResistMangos.MWX.
- Elija .
- En Variables, ingrese ResistRotura.
- Haga clic en Opciones.
- En ¿Qué desea deteminar? (hipótesis alterna), seleccione El valor más pequeño de los datos es un valor atípico.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
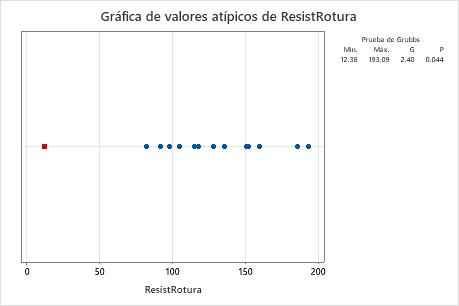
La media de la muestra es 123.4. El estadístico G indica que el valor de datos más pequeño, 12.38, es 2.4 desviaciones estándar menor que la media. El valor p indica que, si todos los valores provienen en realidad de la misma población distribuida normalmente, entonces la probabilidad de obtener un valor mínimo tan pequeño es solo 0.044. Puesto que el valor p de 0.044 es menor que el nivel de significancia (denotado como α o alfa) de 0.05, el ingeniero rechaza la hipótesis nula y concluye que el valor más pequeño es un valor atípico.
El ingeniero investiga y descubre que la persona que ingresó los datos accidentalmente escribió 12.38 en lugar de 123.8.
Método
| Hipótesis nula | Todos los valores de los datos provienen de la misma población normal |
|---|---|
| Hipótesis alterna | El valor más pequeño de los datos es un valor atípico |
| Nivel de significancia | α = 0.05 |
Prueba de Grubbs
| Variable | N | Media | Desv.Est. | Mín. | Máx. | G | P |
|---|---|---|---|---|---|---|---|
| ResistRotura | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
Valor atípico
| Variable | Fila | Valor atípico |
|---|---|---|
| ResistRotura | 10 | 12.38 |