Media
La media describe la muestra con un solo valor que representa el centro de los datos. La media se calcula como el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
N
El tamaño de la muestra (N) es el número total de observaciones en la muestra.
Interpretación
El tamaño de la muestra afecta la potencia de la prueba.
Por lo general, con un tamaño de muestra más grande, la prueba tiene más potencia para detectar una diferencia entre los datos de la muestra y la distribución normal. Es decir, cuando realmente existe una diferencia, usted tiene mayor probabilidad de detectarla con un tamaño de muestra más grande.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos con respecto a la media. Una mayor desviación estándar de la muestra indica que los datos están más dispersos alrededor de la media.
AD
El estadístico de bondad de ajuste de Anderson-Darling (AD) mide el área entre la línea ajustada (basada en la distribución normal) y la función de distribución empírica (que se basa en los puntos de los datos). El estadístico de Anderson-Darling es una distancia elevada al cuadrado que tiene mayor ponderación en las colas de la distribución.
Interpretación
Minitab utiliza el estadístico de Anderson-Darling para calcular el valor p. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula. Valores más grandes del estadístico de Anderson-Darling indican que los datos no siguen la distribución normal.
KS
La prueba de Kolmogorov-Smirnovcom compara la función de distribución acumulada empírica (ECDF) de los datos de la muestra con la distribución esperada si los datos fueran normales.
Interpretación
Minitab utiliza el estadístico de Kolmogorov-Smirnov para calcular el valor p. El valor p es la probabilidad de obtener un estadístico de prueba (tal como el estadístico de Kolmogorov-Smirnov) que es por lo menos tan extremo como el valor que se calcula a partir de la muestra, cuando los datos son normales. Valores más grandes del estadístico de Kolmogorov-Smirnov indican que los datos no siguen la distribución normal.
RJ
El estadístico de Ryan-Joiner mide qué tan bien siguen los datos una distribución normal al calcular la correlación entre los datos y las puntuaciones normales de los datos. Si el coeficiente de correlación está cerca de 1, es probable que la población sea normal. Esta prueba es similar a la prueba de normalidad de Shapiro-Wilk.
Interpretación
Minitab utiliza el estadístico de Ryan-Joiner para calcular el valor p. El valor p es la probabilidad de obtener un estadístico de prueba (como por ejemplo el estadístico de Ryan-Joiner) que es por lo menor tan extremo como el valor que se calcula a partir de la muestra, cuando los datos son normales. Valores más grandes del estadístico de Ryan-Joiner indican que los datos no siguen la distribución normal.
Valor p
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si los datos no siguen una distribución normal.
- Valor p ≤ α: Los datos no siguen una distribución normal (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que sus datos no siguen una distribución normal.
- Valor p > α: Usted no puede concluir que los datos no siguen una distribución normal (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que los datos no siguen una distribución normal.
Gráfica de probabilidad
Una gráfica de probabilidad crea una función de distribución acumulada (CDF) estimada a partir de la muestra al graficar el valor de cada una de las observaciones en función de la probabilidad acumulada estimada de la observación.
Interpretación
Utilice una gráfica de probabilidad para determinar visualmente qué tan bien se ajustan los datos a la distribución normal.
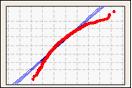
Datos asimétricos hacia la derecha
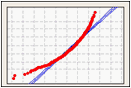
Datos asimétricos hacia la izquierda
Sugerencia
En Minitab, coloque el cursor sobre la línea de distribución ajustada para ver una gráfica de percentiles y valores.
