En este tema
Paso 1: Describir el centro de los datos
Utilice la media para describir la muestra con un solo valor que representa el centro de los datos. Muchos análisis estadísticos utilizan la media como una medida estándar del centro de la distribución de los datos.
La mediana es otra medida del centro de la distribución de los datos. Por lo general, los valores atípicos influyen menos en la mediana que en la media. La mitad de los valores de los datos es mayor que el valor de la mediana y la mitad de los valores de los datos es menor que el valor de la mediana.
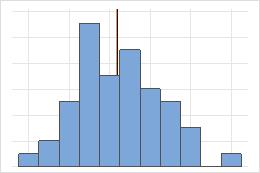
Simétrica
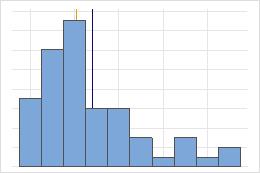
No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
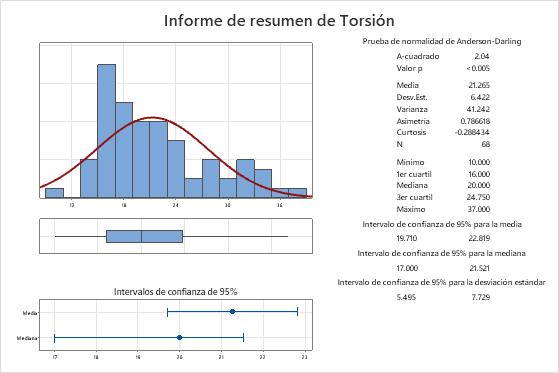
Resultados clave: Media y mediana
En estos resultados, la torsión media que se requiere para retirar la tapa de una crema dental es 21.265 y la torsión mediana es 20. Los datos parecen ser asimétricos hacia la derecha, lo que explica por qué la media es mayor que la mediana.
Paso 2: Determinar un intervalo de confianza para la media, la mediana y la desviación estándar
El intervalo de confianza proporciona un rango de valores probables para el parámetro de población. Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan el parámetro de población.

Resultados clave: Intervalo de confianza para la media, intervalo de confianza para la mediana, intervalo de confianza para la Desv.Est.
- La media de la población para las mediciones de torque está entre 19,710 y 22,819.
- La mediana de la población para las mediciones de torque está entre 17 y 21,521.
- La desviación estándar de la población para las mediciones de torque está entre 5,495 y 7,729.
Paso 3: Evaluar la forma y dispersión de la distribución de los datos
Utilice el histograma y la gráfica de caja para evaluar la forma y dispersión de los datos y para identificar cualquier posible valor atípico.
Examinar la dispersión de los datos para determinar si los datos parecen ser asimétricos
Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
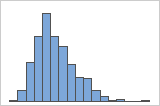
Asimétrico hacia la derecha
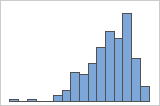
Asimétrico hacia la izquierda
El histograma con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. El histograma con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Identificar valores atípicos
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
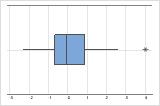
En una gráfica de caja, los asteriscos (*) denotan valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
Buscar datos multimodales
Los datos multimodales tienen múltiples picos, también denominados modas. Los datos multimodales suelen indicar que aún no se han considerado variables importantes.
Si usted tiene información adicional que le permita clasificar las observaciones en grupos, puede crear una variable de grupo con esta información. Luego, puede crear la gráfica con los grupos para determinar si la variable de grupo explica los picos en los datos.
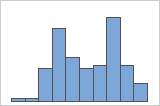
Simple
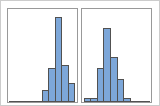
Con grupos
Por ejemplo, un gerente de un banco recolecta datos de tiempos de espera y crea un histograma simple. El histograma parece tener dos picos. Después de una investigación más a fondo, el gerente determina que el tiempo de espera de los clientes que están cobrando un cheque es más corto que el tiempo de espera de los clientes que están solicitando una hipoteca. El gerente agrega una variable de grupo para la tarea que realizan los clientes y luego crea un histograma con grupos.
