En este tema
A-cuadrado
El estadístico de bondad de ajuste de Anderson-Darling (A-cuadrado) mide el área entre la línea ajustada (basada en la distribución normal) y la función de distribución empírica (que se basa en los puntos de los datos). El estadístico de Anderson-Darling es una distancia elevada al cuadrado que tiene mayor ponderación en las colas de la distribución.
Interpretación
Minitab utiliza el estadístico de Anderson-Darling para calcular el valor p. El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula. Un valor más pequeño para el estadístico de Anderson-Darling indica que los datos siguen la distribución normal más de cerca.
Valor p
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si los datos no siguen una distribución normal.
- Valor p ≤ α: Los datos no siguen una distribución normal (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que sus datos no siguen una distribución normal.
- Valor p > α: Usted no puede concluir que los datos no siguen una distribución normal (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que los datos no siguen una distribución normal.
Media
La media es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
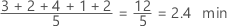
Interpretación
Utilice la media para describir la muestra con un solo valor que representa el centro de los datos. Muchos análisis estadísticos utilizan la media como una medida estándar del centro de la distribución de los datos.
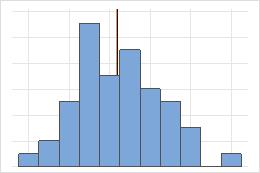
Simétrica
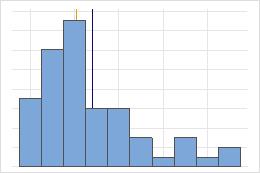
No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
Debido a que la desviación estándar utiliza las mismas unidades que los datos, generalmente es más fácil de interpretar que la varianza.
Interpretación
Utilice la desviación estándar para determinar qué tan dispersos están los datos con respecto a la media. Un valor de desviación estándar más alto indica una mayor dispersión de los datos. Una buena regla empírica para una distribución normal es que aproximadamente 68% de los valores se ubican dentro de una desviación estándar de la media, 95% de los valores se ubican dentro de dos desviaciones estándar y 99.7% de los valores se ubican dentro de tres desviaciones estándar.
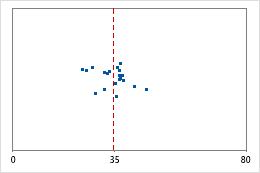
Hospital 1
Hospital 2
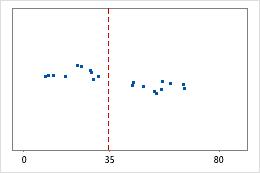
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Varianza
La varianza mide qué tan dispersos están los datos alrededor de su media. La varianza es igual a la desviación estándar elevada al cuadrado.
Interpretación
Mientras mayor sea la varianza, mayor será la dispersión de los datos.
Puesto que la varianza (σ2) es una cantidad elevada al cuadrado, sus unidades también están elevadas al cuadrado, lo que puede dificultar el uso de la varianza en la práctica. La desviación estándar generalmente es más fácil de interpretar porque utiliza las mismas unidades que los datos. Por ejemplo, una muestra del tiempo de espera en una parada de autobuses puede tener una media de 15 minutos y una varianza de 9 minutos2. Debido a que la varianza no está en las mismas unidades que los datos, la varianza suele mostrarse con su raíz cuadrada, la desviación estándar. Una varianza de 9 minutos2 es equivalente a una desviación estándar de 3 minutos.
Asimetría
La asimetría es el grado en que los datos no son simétricos.
Interpretación
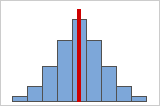
Figura A
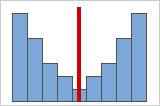
Figura B
Distribuciones simétricas o no asimétricas
A medida que los datos se vuelven más simétricos, el valor de su asimetría se acerca a cero. La figura A muestra datos distribuidos normalmente, que por definición exhiben relativamente poca asimetría. Al dibujar una línea por debajo de la mitad de este histograma de datos normales, se puede ver fácilmente que un lado es el reflejo del otro. Pero la falta de asimetría por sí sola no implica normalidad. La figura B muestra una distribución en la que ambos lados siguen siendo un reflejo el uno del otro, a pesar de que la distribución de los datos dista mucho de ser normal.
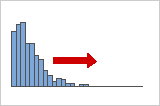
Distribuciones asimétricas positivas o hacia la derecha
Los datos con asimetría positiva o asimétricos hacia la derecha se llaman así porque la "cola" de la distribución apunta hacia la derecha y porque el valor de asimetría es mayor que 0 (es decir, positivo). Los datos sobre salarios suelen ser asimétricos de esta manera: muchos empleados de una empresa ganan relativamente poco, mientras que cada vez menos personas ganan salarios muy elevados.
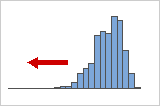
Distribuciones asimétricas negativas o hacia la izquierda
Los datos asimétricos hacia la izquierda o con asimetría negativa se llaman así porque la "cola" de la distribución apunta hacia la izquierda y porque producen un valor de asimetría negativo. Los datos de tasas de fallas suelen ser asimétricos a la izquierda. Consideremos el caso de las bombillas: muy pocas se quemarán inmediatamente, la gran mayoría dura un tiempo considerablemente largo.
Curtosis
La curtosis indica la manera en que las colas de una distribución difieren de la distribución normal.
Interpretación
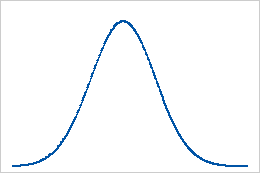
Línea de base: Valor de curtosis de 0
Los datos normalmente distribuidos establecen la línea de base para la curtosis. Un valor de curtosis de 0 indica que los datos siguen perfectamente la distribución normal. Un valor de curtosis que se desvía significativamente de 0 puede indicar que los datos no están distribuidos normalmente.
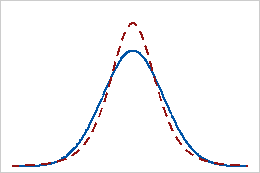
Curtosis positiva
Una distribución que tiene un valor positivo de curtosis indica que la distribución tiene colas más pesadas que la distribución normal. Por ejemplo, los datos que siguen una distribución t tienen un valor positivo de curtosis. La línea continua indica la distribución normal y la línea de puntos indica una distribución que tiene un valor positivo de curtosis.
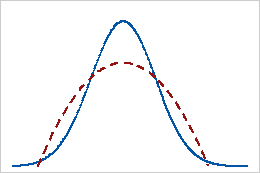
Curtosis negativa
Una distribución con un valor negativo de curtosis indica que la distribución tiene colas más livianas que la distribución normal. Por ejemplo, los datos que siguen una distribución beta con el primer y el segundo parámetro de forma iguales a 2 tienen un valor negativo de curtosis. La línea continua indica la distribución normal y la línea de puntos indica una distribución que tiene un valor negativo de curtosis.
N
El número de valores presentes en la muestra.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Mínimo
El mínimo es el valor más pequeño de los datos.
En estos datos, el mínimo es 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el mínimo para identificar un posible valor atípico o un error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor mínimo es muy bajo, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
1er cuartil
Los cuartiles son los tres valores —el 1er cuartil en 25% (Q1), el segundo cuartil en 50% (Q2 o mediana) y el tercer cuartil en 75% (Q3)— que dividen una muestra de datos ordenados en cuatro partes iguales.
El 1er cuartil es el percentil 25 e indica que 25% de los datos es menor que o igual a este valor.
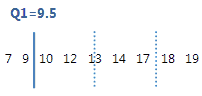
Para estos datos ordenados, el 1er cuartil (Q1) es 9.5. Es decir, 25% de los datos es menor que o igual a 9.5.
Mediana
La mediana es el punto medio del conjunto de datos. El valor de este punto medio es el punto en el cual la mitad de las observaciones está por encima del valor y la otra mitad está por debajo del valor. La mediana se determina jerarquizando las observaciones y hallando la observación que ocupe el número [N + 1] / 2 en el orden jerarquizado. Si el número de observaciones es par, entonces la mediana es el valor promedio de las observaciones jerarquizadas en los números N / 2 y [N / 2] + 1.
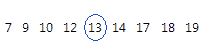
Para estos datos ordenados, la mediana es 13. Es decir, la mitad de los valores es menor que o igual a 13 y la otra mitad de los valores es mayor que o igual a 13. Si usted agrega otra observación igual a 20, la mediana es 13,5, que es el promedio entre la 5ta observación (13) y la 6ta observación (14).
Interpretación

Simétrica

No simétrica
En la distribución simétrica, la media (línea azul) y la mediana (línea naranja) son tan similares que no es fácil distinguir las dos líneas. En cambio, la distribución no simétrica es asimétrica hacia la derecha.
3er cuartil
Los cuartiles son los tres valores —el 1er cuartil en 25% (Q1), el segundo cuartil en 50% (Q2 o mediana) y el tercer cuartil en 75% (Q3)— que dividen una muestra de datos ordenados en cuatro partes iguales.
El tercer cuartil es el percentil 75 e indica que 75% de los datos es menor que o igual a este valor.
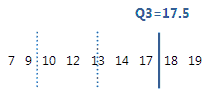
Para estos datos ordenados, el tercer cuartil (Q3) es 17.5. Es decir, 75% de los datos es menor que o igual a 17.5.
Máximo
El máximo es el valor más grande de los datos.
En estos datos, el máximo es 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretación
Utilice el máximo para identificar un posible valor atípico o error de entrada de datos. Una de las maneras más sencillas de evaluar la dispersión de los datos consiste en comparar el mínimo y el máximo. Si el valor máximo es muy alto, incluso cuando considere el centro, la dispersión y la forma de los datos, investigue la causa del valor extremo.
Intervalo de confianza
El intervalo de confianza proporciona un rango de valores probables para el parámetro de población. Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces la muestra, un determinado porcentaje de los intervalos o bordes de confianza resultantes tendría el parámetro de población desconocido. El porcentaje de estos intervalos o bordes de confianza que contiene el parámetro es el nivel de confianza del intervalo. Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan el parámetro de población.
Un borde superior define un valor en comparación con el cual es probable que el parámetro de población sea menor. Un borde inferior define un valor en comparación con el cual es probable que el parámetro de población sea mayor.
El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra. Para obtener más información, vaya a Maneras de obtener un intervalo de confianza más preciso.
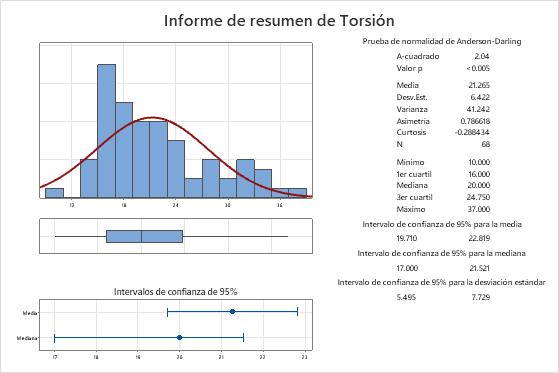
- La media de la población para las mediciones de torque está entre 19,710 y 22,819.
- La mediana de la población para las mediciones de torque está entre 17 y 21,521.
- La desviación estándar de la población para las mediciones de torque está entre 5,495 y 7,729.
Histograma
Un histograma divide los valores de la muestra en muchos intervalos y representa la frecuencia de los valores de datos en cada intervalo con una barra.
Interpretación
Utilice un histograma para evaluar la forma y dispersión de los datos. Los histogramas funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Usted puede utilizar un histograma de los datos con una curva normal sobrepuesta para examinar la normalidad de los datos. Una distribución normal es simétrica y tiene forma de campana, como lo indica la curva. Comúnmente es difícil evaluar la normalidad con muestras pequeñas. Una gráfica de probabilidad es la mejor opción para determinar el ajuste de la distribución.
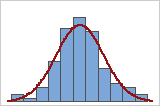
Ajuste adecuado
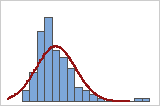
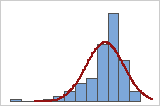
Ajuste deficiente
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
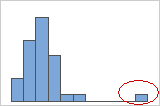
En un histograma, las barras aisladas en cualquiera de los extremos de la gráfica identifican posibles valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
- Datos multimodales
-
Los datos multimodales tienen múltiples picos, también denominados modas. Los datos multimodales suelen indicar que aún no se han considerado variables importantes.
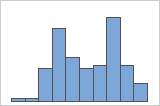
Simple
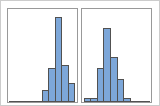
Con grupos
Por ejemplo, un gerente de un banco recolecta datos de tiempos de espera y crea un histograma simple. El histograma parece tener dos picos. Después de una investigación más a fondo, el gerente determina que el tiempo de espera de los clientes que están cobrando un cheque es más corto que el tiempo de espera de los clientes que están solicitando una hipoteca. El gerente agrega una variable de grupo para la tarea que realizan los clientes y luego crea un histograma con grupos.
Si usted tiene información adicional que le permita clasificar las observaciones en grupos, puede crear una variable de grupo con esta información. Luego, puede crear la gráfica con los grupos para determinar si la variable de grupo explica los picos en los datos.
Gráfica de caja
Una gráfica de caja proporciona un resumen gráfico de la distribución de una muestra. La gráfica de caja muestra la forma, tendencia central y variabilidad de los datos.
Interpretación
Utilice una gráfica de caja para examinar la dispersión de los datos y para identificar cualquier posible valor atípico. Las gráficas de caja funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
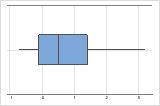
Asimétrico hacia la derecha
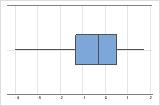
Asimétrico hacia la izquierda
La gráfica de caja con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. La gráfica de caja con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
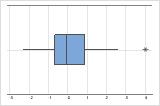
En una gráfica de caja, los asteriscos (*) denotan valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
