Interpretar los resultados clave para Prueba de bondad de ajuste para Poisson

Complete los siguientes pasos para interpretar una prueba de bondad de ajuste para Poisson. La salida clave incluye el valor p y varias gráficas.

En este tema

Paso 1: Determinar si los datos no siguen una distribución de Poisson
Paso 2: Examine la diferencia entre los valores observados y esperados para cada categoría

Paso 1: Determinar si los datos no siguen una distribución de Poisson

Para determinar si los datos no siguen una distribución de Poisson, compare el valor p con su nivel de significancia (α). Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que los datos no siguen una distribución de Poisson cuando los datos sí siguen una distribución de Poisson.

Valor p ≤ α: Los datos no siguen una distribución de Poisson (Rechaza H₀): Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que sus datos no siguen una distribución de Poisson.
Valor p > α: No puede concluir que los datos no siguen una distribución de Poisson (No puede rechazar H₀): Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula porque usted no tiene suficiente evidencia para concluir que los datos no siguen una distribución de Poisson.

Método

Frecuencias en Observados

Estadísticas descriptivas

N	Media
300	0.536667

Conteos observados y esperados para Defectos

Defectos	Probabilidad de Poisson	Conteo observado	Conteo esperado	Contribución a chi-cuadrada
0	0.584694	213	175.408	8.056
1	0.313786	41	94.136	29.993
2	0.084199	18	25.260	2.086
>=3	0.017321	28	5.196	100.072

Prueba de chi-cuadrada

Hipótesis nula	H₀: Los datos siguen una distribución de Poisson
Hipótesis alterna	H₁: Los datos no siguen una distribución de Poisson

GL	Chi-cuadrada	Valor p
2	140.208	0.000

Resultado clave: Valor p

En estos resultados, la hipótesis nula indica que los datos siguen una distribución de Poisson. Puesto que el valor p es 0.000, que es menor que 0.05, la decisión es rechazar la hipótesis nula. Usted puede concluir que los datos no provienen de una distribución de Poisson.

Paso 2: Examine la diferencia entre los valores observados y esperados para cada categoría

Utilice una gráfica de barras de valores observados y esperados para determinar si, para cada categoría, el número de valores observados difiere del número de valores esperados. Diferencias más grandes entre los valores observados y esperados indican que los datos no siguen una distribución de Poisson.

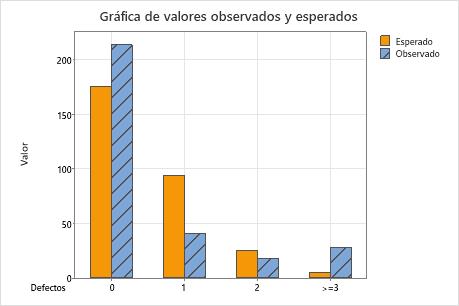
Esta gráfica de barras indica que los valores observados para 0 defectos, 1 defecto y más de 3 defectos son diferentes de los valores esperados. Por lo tanto, la gráfica de barras confirma visualmente lo que indica el valor p, es decir, que los datos no siguen una distribución de Poisson.