En este tema
Media
La media de Poisson es la suma de cada categoría multiplicada por el número de valores observados en esa categoría, dividido entre el número total de valores observados.
N
El número de valores presentes en la muestra.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N*
El número de valores faltantes en la muestra. El número de valores faltantes se refiere a las celdas que contienen el símbolo de valor faltante *.
| Conteo total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Probabilidad de Poisson
La probabilidad para cada categoría, presuponiendo que los datos siguen una distribución de Poisson que tiene una media que es igual a la media de Poisson que se calcula a partir de los datos. Minitab utiliza la probabilidad de Poisson para calcular los valores esperados.
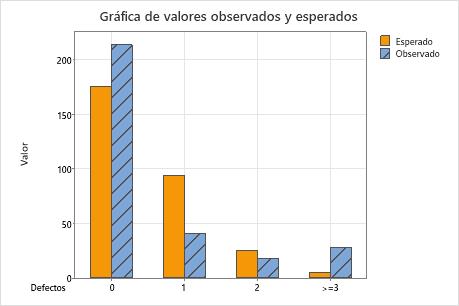
Valores observados y esperados
Los valores observados son el número real de observaciones en una muestra que pertenecen a una categoría.
Los valores esperados son el número de observaciones que se esperarían si las probabilidades de Poisson fueran verdaderas. Minitab calcula los conteos esperados multiplicando las probabilidades de Poisson de cada categoría por el tamaño total de la muestra.
Si los conteos esperados (también llamados frecuencias esperadas) de cualquier categoría son menores que 5, los resultados de la prueba pudieran no ser válidos. Si los conteos esperados de una categoría son demasiado bajos, usted podría combinar esa categoría con categorías adyacentes para alcanzar el conteo esperado mínimo.
Por ejemplo, un departamento de finanzas tiene cinco categorías para clasificar la cantidad de días que las facturas permanecen vencidas: 15 o menos, 16–30, 31–45, 46–60 y 60 o más. La categoría de 60 días o más tiene un conteo esperado bajo, de modo que el departamento de finanzas la combina con la categoría de 46–60 días para crear una categoría combinada de 45 días o más.
Interpretación
Usted puede comparar los valores observados y esperados utilizando la tabla de salida o la gráfica de barras. Diferencias más grandes entre los valores observados y esperados indican que los datos no siguen una distribución de Poisson.
Método
| Frecuencias en Observados |
|---|
Estadísticas descriptivas
| N | Media |
|---|---|
| 300 | 0.536667 |
Conteos observados y esperados para Defectos
| Defectos | Probabilidad de Poisson | Conteo observado | Conteo esperado | Contribución a chi-cuadrada |
|---|---|---|---|---|
| 0 | 0.584694 | 213 | 175.408 | 8.056 |
| 1 | 0.313786 | 41 | 94.136 | 29.993 |
| 2 | 0.084199 | 18 | 25.260 | 2.086 |
| >=3 | 0.017321 | 28 | 5.196 | 100.072 |
Prueba de chi-cuadrada
| Hipótesis nula | H₀: Los datos siguen una distribución de Poisson |
|---|---|
| Hipótesis alterna | H₁: Los datos no siguen una distribución de Poisson |
| GL | Chi-cuadrada | Valor p |
|---|---|---|
| 2 | 140.208 | 0.000 |
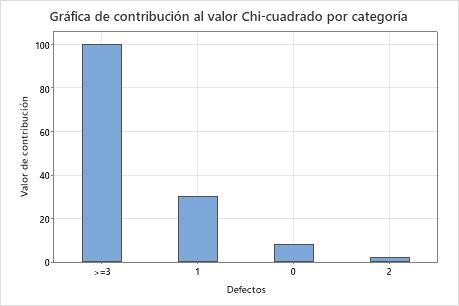
Contribución a chi-cuadrada
Utilice las contribuciones de las categorías individuales para cuantificar qué tanto del estadístico total de chi-cuadrada se puede atribuir a la divergencia de cada categoría.
Minitab calcula la contribución de cada categoría al estadístico de chi-cuadrada como el cuadrado de la diferencia entre los valores observados y esperados para una categoría dividido entre el valor esperado para esa categoría. El estadístico de chi-cuadrada es la suma de estos valores para todas las categorías.
Interpretación
Las categorías con una diferencia grande entre los valores observados y esperados hacen una contribución más grande al estadístico general de chi-cuadrada.
Método
| Frecuencias en Observados |
|---|
Estadísticas descriptivas
| N | Media |
|---|---|
| 300 | 0.536667 |
Conteos observados y esperados para Defectos
| Defectos | Probabilidad de Poisson | Conteo observado | Conteo esperado | Contribución a chi-cuadrada |
|---|---|---|---|---|
| 0 | 0.584694 | 213 | 175.408 | 8.056 |
| 1 | 0.313786 | 41 | 94.136 | 29.993 |
| 2 | 0.084199 | 18 | 25.260 | 2.086 |
| >=3 | 0.017321 | 28 | 5.196 | 100.072 |
Prueba de chi-cuadrada
| Hipótesis nula | H₀: Los datos siguen una distribución de Poisson |
|---|---|
| Hipótesis alterna | H₁: Los datos no siguen una distribución de Poisson |
| GL | Chi-cuadrada | Valor p |
|---|---|---|
| 2 | 140.208 | 0.000 |
En estos resultados, los valores de chi-cuadrada de cada categoría se suman al estadístico general de chi-cuadrada, que es 140.208. La contribución más grande proviene de la categoría de 3 o más defectos. Este resultado indica que la diferencia más grande entre los conteos observados y esperados está en la categoría de 3 o más defectos. La diferencia más pequeña entre los conteos observados y esperados está en la categoría de 2 defectos.
Hipótesis nula y alternativa
- Hipótesis nula
- La hipótesis nula indica que una población sigue una distribución específica. La hipótesis nula suele ser una afirmación inicial que se basa en análisis previos o en conocimiento especializado.
- Hipótesis alternativa
- La hipótesis alternativa establece que una población no sigue una distribución específica.
GL
Los grados de libertad (GL) son el número de informaciones independientes sobre un estadístico. Los grados de libertad para la prueba de bondad de ajuste para Poisson es el número de categorías – 2.
Interpretación
Minitab utiliza los grados de libertad para determinar el estadístico de prueba. Mientras más categorías incluya usted en el estudio, más grados de libertad tendrá.
Chi-cuadrado
El estadístico de chi-cuadrada es un estadístico de prueba que mide la cantidad de divergencia entre la distribución de los datos de su muestra y la distribución de Poisson esperada.
Interpretación
Usted puede utilizar el estadístico de chi-cuadrada para determinar si puede rechazar la hipótesis nula. Sin embargo, el valor p se utiliza con mayor frecuencia debido a que es más fácil de interpretar. El valor p es la probabilidad de obtener un estadístico de prueba (como el estadístico de chi-cuadrada) que sea por lo menos tan extremo como el valor calculado a partir de la muestra, cuando los datos siguen una distribución de Poisson.
Para determinar si rechaza la hipótesis nula, compare el estadístico de chi-cuadrada con su valor crítico. Si el estadístico de chi-cuadrada es mayor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula. Puede calcular el valor crítico en Minitab o buscar el valor crítico en una tabla de distribución de chi-cuadrada en la mayoría de los libros de estadística. Para obtener más información, vaya a Uso de la función de distribución acumulada inversa (ICDF) y haga clic en "Usar la ICDF para calcular los valores críticos".
Minitab utiliza el estadístico de chi-cuadrada para calcular el valor p.
Valor p
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si los datos no siguen una distribución de Poisson.
- Valor p ≤ α: Los datos no siguen una distribución de Poisson (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula y concluir que sus datos no siguen una distribución de Poisson.
- Valor p > α: No puede concluir que los datos no siguen una distribución de Poisson (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula porque usted no tiene suficiente evidencia para concluir que los datos no siguen una distribución de Poisson.
Gráfica de contribución al valor de chi-cuadrada por categoría
Esta gráfica de barras muestra la contribución de cada categoría al estadístico general de chi-cuadrada. Usted puede elegir una gráfica que ordene las categorías por contribución, desde la contribución más grande hasta la contribución más pequeña.
Interpretación
Las categorías con una diferencia grande entre los valores observados y esperados hacen una contribución más grande al estadístico general de chi-cuadrada.

Esta gráfica de barras indica que la diferencia más grande entre los valores esperados y observados está en la categoría de 3 o más defectos.
Gráfica de valores observados y esperados
Utilice una gráfica de barras de valores observados y esperados para determinar si, para cada categoría, el número de valores observados difiere del número de valores esperados. Diferencias más grandes entre los valores observados y esperados indican que los datos no siguen una distribución de Poisson.

Esta gráfica de barras indica que los valores observados para 0 defectos, 1 defecto y más de 3 defectos son diferentes de los valores esperados. Por lo tanto, la gráfica de barras confirma visualmente lo que indica el valor p, es decir, que los datos no siguen una distribución de Poisson.
