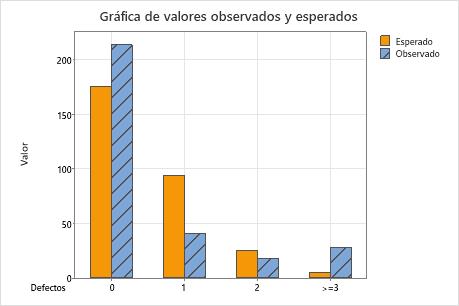
Un ingeniero especializado en calidad que trabaja en una empresa de productos electrónicos de consumo desea saber si los defectos por cada televisor provienen de una distribución de Poisson. El ingeniero selecciona 300 televisores de forma aleatoria y registra el número de defectos por aparato.
- Abra los datos de muestra, DefectosTV.MTW.
- Elija .
- En Variable, ingrese Defectos.
- En Variable de frecuencia: (opcional), ingrese Observados.
- Haga clic en Aceptar.
Interpretar los resultados
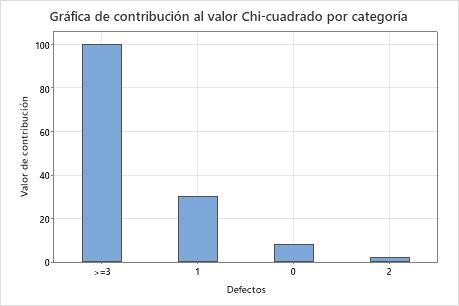
La hipótesis nula indica que los datos siguen una distribución de Poisson. Puesto que el valor p es 0.000, que es menor que el nivel de significancia de 0.05, el ingeniero rechaza la hipótesis nula y concluye que los datos no siguen una distribución de Poisson. Las gráficas indican que la diferencia entre los valores observados y esperados es grande para las categorías 1 y 
3 y que la categoría 3 es la que más contribuye al estadístico de chi-cuadrada.
Método
| Frecuencias en Observados |
|---|
Estadísticas descriptivas
| N | Media |
|---|---|
| 300 | 0.536667 |
Conteos observados y esperados para Defectos
| Defectos | Probabilidad de Poisson | Conteo observado | Conteo esperado | Contribución a chi-cuadrada |
|---|---|---|---|---|
| 0 | 0.584694 | 213 | 175.408 | 8.056 |
| 1 | 0.313786 | 41 | 94.136 | 29.993 |
| 2 | 0.084199 | 18 | 25.260 | 2.086 |
| >=3 | 0.017321 | 28 | 5.196 | 100.072 |
Prueba de chi-cuadrada
| Hipótesis nula | H₀: Los datos siguen una distribución de Poisson |
|---|---|
| Hipótesis alterna | H₁: Los datos no siguen una distribución de Poisson |
| GL | Chi-cuadrada | Valor p |
|---|---|---|
| 2 | 140.208 | 0.000 |
