Ejemplo de Mostrar estadísticos descriptivos

Un ingeniero especializado en control de calidad debe garantizar que las tapas de las botellas de champú queden ajustadas correctamente. Si las tapas quedan flojas, podrían caerse durante el envío. Si se aprietan demasiado, será difícil retirarlas. El valor objetivo del par de torsión para ajustar las tapas es 18. El ingeniero recolecta una muestra aleatoria de 68 botellas y prueba la cantidad de par de torsión que se necesita para quitar las tapas.

Como parte de la investigación inicial, el ingeniero analiza los estadísticos descriptivos de las mediciones del par de torsión para evaluar la distribución de los datos de cada máquina.

Abra los datos de muestra, TorsiónTapa.MTW.
Elija Estadísticas > Estadísticas básicas > Mostrar estadísticos descriptivos.
En Variables, ingrese Torsión.
En Por variables (opcional), ingrese Máquina.
Haga clic en el botón Gráficas y luego seleccione Histograma de datos, Gráfica de valores individuales y Gráfica de caja de datos.
Haga clic en Aceptar en cada cuadro de diálogo.

Interpretar los resultados

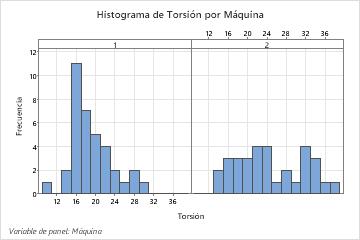
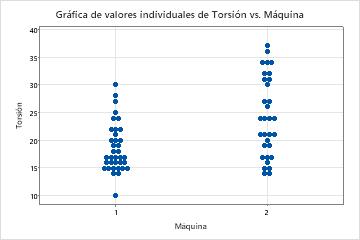
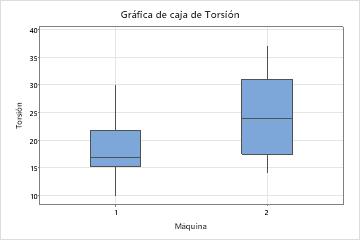
La media del valor de torsión de la Máquina 1 está más cerca del objetivo de 18 que la media del valor de torsión de la Máquina 2. La torsión media requerida para retirar las tapas de la Máquina 1 es 18,667 y la torsión media requerida para retirar las tapas de la Máquina 2 es 24,19. La distribución de los datos de la Máquina 1 también es menos variable. La desviación estándar es 4.395 para la Máquina 1 y 7.12 para la Máquina 2.

Las gráficas también muestran que hay una diferencia en los valores medios de torsión de las dos máquinas. Para determinar si existe una diferencia significativa en las medias de las poblaciones, el ingeniero podría realizar una prueba t de 2 muestras.

Estadísticas

Variable	Máquina	N	N*	Media	Error estándar de la media	Desv.Est.	Mínimo	Q1	Mediana	Q3
Torsión	1	36	0	18.6667	0.732467	4.39480	10	15.25	17	21.75
	2	32	0	24.1875	1.25839	7.11852	14	17.5	24	31

Variable	Máquina	Máximo
Torsión	1	30
	2	37