En este tema
Coeficiente de correlación de Pearson
Fórmula
Mide el grado de relación lineal entre dos variables. El coeficiente de correlación presupone un valor entre −1 y +1. Si una variable tiende a aumentar mientras la otra disminuye, el coeficiente de correlación es negativo. En cambio, si las dos variables tienden a aumentar al mismo tiempo, el coeficiente de correlación es positivo.
Para las variables x y y:
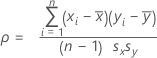
Notación
| Término | Description |
|---|---|
 | media de la muestra para la primera variable |
| sx | desviación estándar simple para la primera variable |
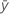 | media de la muestra para la segunda variable |
| sy | desviación estándar de la muestra para la segunda variable |
| n | número de observaciones |
Intervalos de confianza de correlación de Pearson
El intervalo de confianza bilateral de (1− α)100% para ρ es (ρL, ρU), donde el límite inferior, ρL, y el límite superior, ρU, se definen de la siguiente manera:

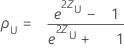
donde:


Notación
| Término | Description |
|---|---|
| r | La estimación de la correlación de la muestra de Pearson de la correlación desconocida, ρ |
| ρ | coeficiente de correlación |
| n | número de observaciones |
Coeficiente de correlación de Spearman
Para calcular el coeficiente de correlación de Spearman y el valor p, realice una correlación de Pearson con los rangos de los datos. Los rangos de respuestas iguales son el promedio de los rangos de los empates. La siguiente tabla muestra los rangos de dos muestras de datos.
| C1 | C2 | C3 | C4 |
|---|---|---|---|
| A | Rango A | B | Rango B |
| 45 | 4 | 23 | 1 |
| 78 | 6 | 25 | 3 |
| 24 | 3 | 25 | 3 |
| 51 | 5 | 25 | 3 |
| 13 | 1.5 | 34 | 6 |
| 13 | 1.5 | 30 | 5 |
El coeficiente de correlación de Spearman entre A y B es −0.678 y el valor p es 0.139. Estos valores son idénticos al coeficiente y el valor p de una correlación de Pearson con los valores del Rango A y del Rango B.
Minitab omite de los cálculos las filas que contienen datos faltantes para una o ambas variables. Ambas columnas deben tener el mismo número de filas.
Intervalos de confianza de correlación de Spearman
El intervalo de confianza bilateral de (1− α)100% para ρ es (ρL, ρU), donde el límite inferior, ρL, y el límite superior, ρU, se definen de la siguiente manera:
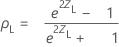
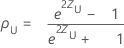
donde:


Bonnett y Wright (2000) sugieren utilizar el siguiente ajuste al error estándar:
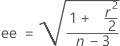
Notación
| Término | Description |
|---|---|
| r | La estimación de la correlación de la muestra de Spearman de la correlación desconocida ρ |
| ρ | coeficiente de correlación |
| n | número de filas con datos presentes para el par de variables |
Valor p
Las hipótesis de una prueba de que la correlación es 0 son las siguientes:
H0: ρ = 0 versus H1: ρ ≠ 0 donde ρ es el coeficiente de correlación de Pearson o el coeficiente de correlación de Spearman entre un par de variables.
Fórmula
El estadístico de prueba para el coeficiente de correlación de Pearson y el coeficiente de correlación de Spearman tienen la misma fórmula.

El valor p es 2 × P(T > t), donde T sigue una distribución t con n – 2 grados de libertad.
Notación
| Término | Description |
|---|---|
| r | coeficiente de correlación de la muestra |
| n | número de observaciones |
