En este tema
Paso 1: Examinar las relaciones entre las variables en una gráfica de matriz
Utilice la gráfica de matriz para examinar las relaciones entre dos variables continuas. Busque también valores atípicos en las relaciones. Los valores atípicos pueden influir en gran medida en los resultados del coeficiente de correlación de Pearson.
Determinar si las relaciones son lineales, monótonas o ninguna de estas. Los siguientes son ejemplos de tipos de formas que describen los coeficientes de correlación. El coeficiente de correlación de Pearson es adecuado para formas lineales. El coeficiente de correlación de Spearman es adecuado para formas monótonas.

Ninguna relación
Los puntos se ubican de forma aleatoria en la gráfica, lo que significa que no existe relación lineal entre las variables.
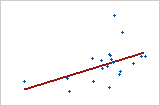
Relación positiva moderada
Algunos puntos están cerca de la línea, pero otros puntos están lejos de ella, lo que indica que solo existe una relación lineal moderada entre las variables.
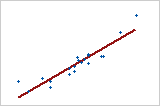
Relación positiva grande
Los puntos se ubican cerca de la línea, lo que indica que existe una relación lineal fuerte entre las variables. La relación es positiva porque a medida que una variable aumenta, la otra variable también aumenta.
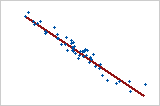
Relación negativa grande
Los puntos se ubican cerca de la línea, lo que indica que existe una relación negativa fuerte entre las variables. La relación es negativa porque a medida que una variable aumenta, la otra variable disminuye.
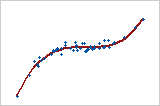
Monótona
En una relación monótona, las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante. En una relación lineal, las variables se mueven en la misma dirección a un ritmo constante. Esta gráfica muestra que ambas variables aumentan al mismo tiempo, pero no al mismo ritmo. Esta relación es monótona, pero no lineal. El coeficiente de correlación de Pearson para estos datos es 0,843, pero la correlación de Spearman es mayor, 0,948.
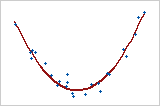
Curva cuadrática
Este ejemplo muestra una relación curva. A pesar de que la relación entre las variables es fuerte, el coeficiente de correlación estaría cerca de cero. La relación no es lineal ni monótona.
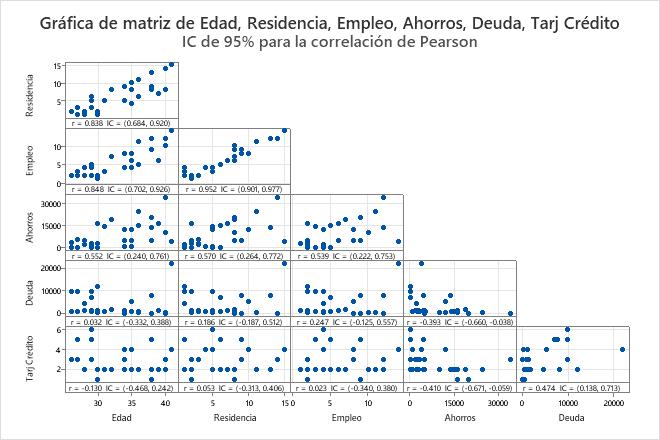
Resultado clave: Gráfica de matriz
- Existe una relación lineal positiva fuerte entre Empleo y Residencia.
- Existe una relación lineal negativa débil entre Tarjetas de crédito y Ahorros.
- Deuda parece tener un valor atípico que debería investigarse.
Paso 2: Examinar los coeficientes de correlación entre las variables
Utilice el coeficiente de correlación de Pearson para examinar la fuerza y la dirección de la relación lineal entre dos variables continuas.
- Resistencia
-
El valor del coeficiente de correlación puede variar de −1 a +1. Mientras mayor sea el valor absoluto del coeficiente, más fuerte será la relación entre las variables.
Para la correlación de Pearson, un valor absoluto de 1 indica una relación lineal perfecta. Una correlación cercana a 0 indica que no existe relación lineal entre las variables. - Dirección:
-
El signo del coeficiente indica la dirección de la relación. Si ambas variables tienden a aumentar o disminuir a la vez, el coeficiente es positivo y la línea que representa la correlación forma una pendiente hacia arriba. Si una variable tiende a incrementarse mientras la otra disminuye, el coeficiente es negativo y la línea que representa la correlación forma una pendiente hacia abajo.
- Nunca se debe concluir que los cambios en una variable causan cambios en otra basándose solamente en la correlación. Solo los experimentos controlados adecuadamente permiten determinar si una relación es causal.
- El coeficiente de correlación de Pearson es muy sensible a valores de datos extremos. Un solo valor que sea muy diferente de los otros valores en un conjunto de datos puede cambiar considerablemente el valor del coeficiente. Usted debe tratar de identificar la causa de cualquier valor extremo. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos que estén asociados con eventos anormales y únicos (causas especiales). Luego, repita el análisis.
- Un coeficiente de correlación de Pearson bajo no significa que no exista relación entre las variables. Las variables pueden tener una relación no lineal.
Método
| Tipo de correlación | Pearson |
|---|---|
| Número de filas utilizadas: | 30 |
Correlaciones
| Edad | Residencia | Empleo | Ahorros | Deuda | |
|---|---|---|---|---|---|
| Residencia | 0.838 | ||||
| Empleo | 0.848 | 0.952 | |||
| Ahorros | 0.552 | 0.570 | 0.539 | ||
| Deuda | 0.032 | 0.186 | 0.247 | -0.393 | |
| Tarj Crédito | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
Resultado clave: Correlación de Pearson
- Residencia y Edad, 0.838
- Empleo y Edad, 0.848
- Empleo y Residencia, 0.952
- Deuda y Ahorros, −0.393
- Tarjetas de crédito y Edad, −0.130
- Tarjetas de crédito y Ahorros, −0.410
