En este tema
Correlaciones de Pearson
La matriz de correlación muestra los valores de correlación, que miden el grado de relación lineal entre cada par de variables. Los valores de correlación se pueden ubicar entre -1 y +1. Si las dos variables tienden a aumentar o disminuir al mismo tiempo, el valor de correlación es positivo. Si una variable aumenta mientras la otra variable disminuye, el valor de correlación es negativo.
Interpretación
Utilice la matriz de correlación para evaluar la fuerza y dirección de la relación entre dos variables. Un valor de correlación alto y positivo indica que las variables miden la misma característica. Si los elementos no están altamente correlacionados, entonces los elementos pudieran medir diferentes características o no estar claramente definidos.
Correlaciones
| Edad | Residencia | Empleo | Ahorros | Deuda | |
|---|---|---|---|---|---|
| Residencia | 0.838 | ||||
| Empleo | 0.848 | 0.952 | |||
| Ahorros | 0.552 | 0.570 | 0.539 | ||
| Deuda | 0.032 | 0.186 | 0.247 | -0.393 | |
| Tarj Crédito | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
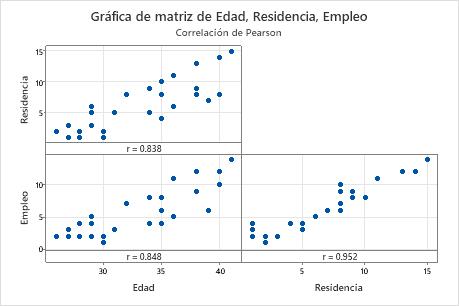
- Residencia y Edad, 0.838
- Empleo y Edad, 0.848
- Empleo y Residencia, 0.952
- Deuda y Ahorros, −0.393
- Tarjetas de crédito y Edad, −0.130
- Tarjetas de crédito y Ahorros, −0.410
Correlaciones de Spearman
Utilice el coeficiente de correlación de Spearman para examinar la fuerza y la dirección de la relación monótona entre dos variables continuas u ordinales. En una relación monótona, las variables tienden a moverse en la misma dirección relativa, pero no necesariamente a un ritmo constante. Para calcular la correlación de Spearman, Minitab jerarquiza los datos sin procesar. Luego, Minitab calcula el coeficiente de correlación con los datos jerarquizados.
- Resistencia
-
El valor del coeficiente de correlación puede variar de −1 a +1. Mientras mayor sea el valor absoluto del coeficiente, más fuerte será la relación entre las variables.
Para la correlación de Spearman, un valor absoluto de 1 indica que los datos ordenados por rango son perfectamente lineales. Por ejemplo, una correlación de Spearman de −1 significa que el valor más alto de la Variable A está asociado con el valor más bajo de la Variable B, el segundo valor más alto de la Variable A está asociado con el segundo valor más bajo de la Variable B y así sucesivamente.
- Dirección:
-
El signo del coeficiente indica la dirección de la relación. Si ambas variables tienden a aumentar o disminuir a la vez, el coeficiente es positivo y la línea que representa la correlación forma una pendiente hacia arriba. Si una variable tiende a incrementarse mientras la otra disminuye, el coeficiente es negativo y la línea que representa la correlación forma una pendiente hacia abajo.
Las siguientes gráficas muestran datos con valores específicos del coeficiente de correlación de Spearman para ilustrar diferentes patrones en la fuerza y la dirección de las relaciones entre las variables.

Ninguna relación: Rho de Spearman = 0
Los puntos se ubican de forma aleatoria en la gráfica, lo que indica que no existe relación entre las variables.
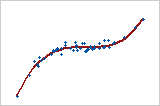
Relación positiva fuerte: Rho de Spearman = 0,948
Los puntos se ubican cerca de la línea, lo que indica que existe una fuerte relación entre las variables. La relación es positiva porque las variables aumentan al mismo tiempo.

Relación negativa fuerte: Rho de Spearman = -1,0
Los puntos se ubican cerca de la línea, lo que indica que existe una fuerte relación entre las variables. La relación es negativa porque a medida que una variable aumenta, la otra variable disminuye.
Nunca se debe concluir que los cambios en una variable causan cambios en otra basándose solamente en la correlación. Solo los experimentos controlados adecuadamente permiten determinar si una relación es causal.
Interpretación
Correlaciones
| Edad | Residencia | Empleo | Ahorros | Deuda | |
|---|---|---|---|---|---|
| Residencia | 0.824 | ||||
| Empleo | 0.830 | 0.912 | |||
| Ahorros | 0.570 | 0.571 | 0.496 | ||
| Deuda | -0.198 | -0.142 | -0.056 | -0.605 | |
| Tarj Crédito | -0.179 | 0.069 | 0.036 | -0.480 | 0.353 |
Correlaciones en parejas de Spearman
| Muestra 1 | Muestra 2 | N | Correlación | IC de 95% para ρ | Valor p |
|---|---|---|---|---|---|
| Residencia | Edad | 30 | 0.824 | (0.624, 0.922) | 0.000 |
| Empleo | Edad | 30 | 0.830 | (0.636, 0.926) | 0.000 |
| Ahorros | Edad | 30 | 0.570 | (0.236, 0.783) | 0.001 |
| Deuda | Edad | 30 | -0.198 | (-0.524, 0.178) | 0.293 |
| Tarj Crédito | Edad | 30 | -0.179 | (-0.508, 0.197) | 0.345 |
| Empleo | Residencia | 30 | 0.912 | (0.798, 0.963) | 0.000 |
| Ahorros | Residencia | 30 | 0.571 | (0.237, 0.784) | 0.001 |
| Deuda | Residencia | 30 | -0.142 | (-0.479, 0.232) | 0.454 |
| Tarj Crédito | Residencia | 30 | 0.069 | (-0.300, 0.419) | 0.719 |
| Ahorros | Empleo | 30 | 0.496 | (0.144, 0.737) | 0.005 |
| Deuda | Empleo | 30 | -0.056 | (-0.408, 0.311) | 0.768 |
| Tarj Crédito | Empleo | 30 | 0.036 | (-0.328, 0.392) | 0.849 |
| Deuda | Ahorros | 30 | -0.605 | (-0.804, -0.283) | 0.000 |
| Tarj Crédito | Ahorros | 30 | -0.480 | (-0.726, -0.124) | 0.007 |
| Tarj Crédito | Deuda | 30 | 0.353 | (-0.020, 0.639) | 0.056 |
En estos resultados, la correlación de Spearman entre Residencia y Edad es 0.824, lo que indica que existe una relación positiva entre las variables. El intervalo de confianza de rho es de 0.624 a 0.922. El valor p es 0.000, lo que indica que la relación es estadísticamente significativa en el nivel de α = 0.05.
La correlación de Spearman entre Deuda y Ahorros es -0.605 y entre Tarjetas de crédito y Ahorros es -0.480. La relación entre estas variables es negativa, lo que indica que a medida que Deuda y Tarjetas de crédito aumentan, Ahorros disminuye.
Filas utilizadas
El número de filas utilizadas se muestra en la tabla Método. Es el número de filas de datos, incluidos los valores faltantes.
Cuando usted tiene valores faltantes, el número de filas utilizado no es igual que el tamaño de la muestra real que se usa en el cálculo del intervalo de confianza.
Intervalos de confianza para Correlación
El intervalo de confianza proporciona un rango de valores probables para los coeficientes de correlación. Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces la muestra, un determinado porcentaje de los intervalos o bordes de confianza resultantes contendría el coeficiente de correlación desconocido. El porcentaje de estos intervalos o bordes de confianza que contiene el coeficiente de correlación es el nivel de confianza del intervalo.
Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan el coeficiente de correlación.
Un borde superior define un valor en comparación con el cual es probable que la diferencia de población sea menor. Un borde inferior define un valor en comparación con el cual es probable que la diferencia de población sea mayor.
Los intervalos de confianza para la correlación de Pearson son sensibles a la normalidad de la distribución bivariada subyacente. Si los datos se desvían de la normalidad, entonces los intervalos de confianza podrían ser inexactos, independientemente de la magnitud del tamaño de la muestra.
Los intervalos de confianza para las correlaciones de Spearman se basan en rangos y son menos sensibles al supuesto de la distribución bivariada subyacente.
Interpretación
El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra. Para obtener más información, vaya a Maneras de obtener un intervalo de confianza más preciso.
Correlaciones en parejas de Pearson
| Muestra 1 | Muestra 2 | N | Correlación | IC de 95% para ρ | Valor p |
|---|---|---|---|---|---|
| Residencia | Edad | 30 | 0.838 | (0.684, 0.920) | 0.000 |
| Empleo | Edad | 30 | 0.848 | (0.702, 0.926) | 0.000 |
| Ahorros | Edad | 30 | 0.552 | (0.240, 0.761) | 0.002 |
| Deuda | Edad | 30 | 0.032 | (-0.332, 0.388) | 0.865 |
| Tarj Crédito | Edad | 30 | -0.130 | (-0.468, 0.242) | 0.494 |
| Empleo | Residencia | 30 | 0.952 | (0.901, 0.977) | 0.000 |
| Ahorros | Residencia | 30 | 0.570 | (0.264, 0.772) | 0.001 |
| Deuda | Residencia | 30 | 0.186 | (-0.187, 0.512) | 0.326 |
| Tarj Crédito | Residencia | 30 | 0.053 | (-0.313, 0.406) | 0.779 |
| Ahorros | Empleo | 30 | 0.539 | (0.222, 0.753) | 0.002 |
| Deuda | Empleo | 30 | 0.247 | (-0.125, 0.557) | 0.189 |
| Tarj Crédito | Empleo | 30 | 0.023 | (-0.340, 0.380) | 0.906 |
| Deuda | Ahorros | 30 | -0.393 | (-0.660, -0.038) | 0.032 |
| Tarj Crédito | Ahorros | 30 | -0.410 | (-0.671, -0.059) | 0.024 |
| Tarj Crédito | Deuda | 30 | 0.474 | (0.138, 0.713) | 0.008 |
En estos resultados, Residencia y Edad tienen una correlación lineal positiva de 0.838. Usted puede estar 95% seguro de que el coeficiente de correlación de la población está entre aproximadamente 0.684 y 0.920. Generalmente, cuando la correlación es más fuerte, el intervalo de confianza es más estrecho. Por ejemplo, Tarjetas de crédito y Edad tienen una débil correlación y el intervalo de confianza de 95% varía de -0.468 a 0.242.
Valor p
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si el coeficiente de correlación es estadísticamente significativo.
- Valor p ≤ α: La correlación entre las medias es estadísticamente significativa (Rechace H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula. Se puede concluir que la correlación es estadísticamente significativa. Utilice su conocimiento especializado para determinar si la diferencia es significativa desde el punto de vista práctico. Para obtener más información, vaya a Significancia estadística y práctica.
- Valor p > α: La correlación no es estadísticamente significativa (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. No cuenta con suficiente evidencia para concluir que la correlación es estadísticamente significativa.
Los procedimientos del valor p para tanto la correlación de Pearson como la correlación de Spearman son robustos ante desviaciones de la normalidad. Los valores p generalmente son exactos para n ≥ 25, independientemente de la población de origen de la población.
Correlaciones en parejas de Pearson
| Muestra 1 | Muestra 2 | N | Correlación | IC de 95% para ρ | Valor p |
|---|---|---|---|---|---|
| Residencia | Edad | 30 | 0.838 | (0.684, 0.920) | 0.000 |
| Empleo | Edad | 30 | 0.848 | (0.702, 0.926) | 0.000 |
| Ahorros | Edad | 30 | 0.552 | (0.240, 0.761) | 0.002 |
| Deuda | Edad | 30 | 0.032 | (-0.332, 0.388) | 0.865 |
| Tarj Crédito | Edad | 30 | -0.130 | (-0.468, 0.242) | 0.494 |
| Empleo | Residencia | 30 | 0.952 | (0.901, 0.977) | 0.000 |
| Ahorros | Residencia | 30 | 0.570 | (0.264, 0.772) | 0.001 |
| Deuda | Residencia | 30 | 0.186 | (-0.187, 0.512) | 0.326 |
| Tarj Crédito | Residencia | 30 | 0.053 | (-0.313, 0.406) | 0.779 |
| Ahorros | Empleo | 30 | 0.539 | (0.222, 0.753) | 0.002 |
| Deuda | Empleo | 30 | 0.247 | (-0.125, 0.557) | 0.189 |
| Tarj Crédito | Empleo | 30 | 0.023 | (-0.340, 0.380) | 0.906 |
| Deuda | Ahorros | 30 | -0.393 | (-0.660, -0.038) | 0.032 |
| Tarj Crédito | Ahorros | 30 | -0.410 | (-0.671, -0.059) | 0.024 |
| Tarj Crédito | Deuda | 30 | 0.474 | (0.138, 0.713) | 0.008 |
En estos resultados, hay muchos valores p que son menores que el nivel de significancia de 0.05, lo cual indica que los coeficientes de correlación de Pearson son estadísticamente significativos.
Nota
Hay casos en que, debido a puntos de datos extremos, el valor p pudiera ser pequeño, pero el intervalo de confianza es muy ancho. Por ejemplo, con Tarjetas de crédito y Deuda, el IC de 95% es muy ancho, pero el valor p es pequeño. Cuando usted examina la gráfica de matriz, puede ver un punto de los datos extremo.
Gráfica de matriz
Una gráfica de matriz es un arreglo de gráficas de dispersión. Cada gráfica de dispersión en la matriz grafica las puntuaciones de un par de elementos en los ejes X y Y.
Interpretación
Utilice la gráfica para evaluar visualmente la relación entre cada combinación de variables. Las relaciones pueden ser lineales, monótonas o ninguna de estas. Utilice también la gráfica de matriz para buscar valores atípicos que pueden influir en gran medida en los resultados. Para obtener más información sobre los tipos de relaciones, vaya a Relaciones lineales, no lineales y monótonas.
Esta gráfica de matriz sugiere que todos los pares de elementos tienen una relación lineal positiva.