En este tema
Hipótesis nula e hipótesis alternativa
- Hipótesis nula
- La hipótesis nula indica que un parámetro de población (tal como la media, la desviación estándar, etc.) es igual a un valor hipotético. La hipótesis nula suele ser una afirmación inicial que se basa en análisis previos o en conocimiento especializado.
- Hipótesis alternativa
- La hipótesis alternativa establece que un parámetro de población es más pequeño, más grande o diferente del valor hipotético de la hipótesis nula. La hipótesis alternativa es lo que usted podría pensar que es cierto o espera probar que es cierto.
Interpretación
En la salida, las hipótesis nula y alternativa le ayudan a verificar que usted ingresó el valor correcto de la relación hipotética.
Nivel de significancia
El nivel de significancia (denotado como α o alfa) es el máximo nivel de riesgo aceptable de rechazar la hipótesis nula cuando la hipótesis nula es verdadera (error tipo I). Por lo general, usted elige el nivel de significancia antes de analizar los datos. En Minitab, puede elegir el nivel de significancia especificando el nivel de confianza, porque el nivel de significancia es igual a 1 menos el nivel de confianza. Puesto que el nivel de confianza predeterminado en Minitab es 0.95, el nivel de significancia predeterminado es 0.05.
Interpretación
Compare el nivel de significancia con el valor p para decidir si puede rechazar o no la hipótesis nula (H0). Si el valor p es menor que el nivel de significancia, la interpretación habitual es que los resultados son estadísticamente significativos y usted rechaza H0.
- Elija un nivel de significancia más alto, como por ejemplo 0.10, para estar más seguro de detectar cualquier diferencia que pueda existir. Por ejemplo, un ingeniero especializado en calidad compara la estabilidad de nuevos rodamientos de esferas con la estabilidad de los rodamientos actuales. El ingeniero debe estar sumamente seguro de que los nuevos rodamientos de esferas son estables, porque rodamientos inestables podrían causar un desastre. Escoge un nivel de significancia de 0.10 para estar más seguro de detectar cualquier posible diferencia en la estabilidad de los rodamientos.
- Elija un nivel de significancia más bajo, como por ejemplo 0.01, para estar más seguro de detectar solo una diferencia que realmente exista. Por ejemplo, un científico de una compañía farmacéutica debe estar muy seguro de que la afirmación de que el nuevo medicamento de la empresa reduce significativamente los síntomas es verdadera. El científico escoge un nivel de significancia de 0.001 para estar más seguro de que existe una diferencia significativa en los síntomas.
N
El tamaño de la muestra (N) es el número total de observaciones en la muestra.
Interpretación
El tamaño de la muestra afecta el intervalo de confianza y la potencia de la prueba.
Generalmente, un tamaño de la muestra más grande da como resultado un intervalo de confianza más estrecho. Con un tamaño de la muestra más grande, la prueba también tendrá más potencia para detectar una diferencia. Para obtener más información, vaya a ¿Qué es potencia?.
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos alrededor de la media. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra. La variación que es aleatoria o natural de un proceso se conoce comúnmente como ruido.
La desviación estándar utiliza las mismas unidades que los datos.
Interpretación
La desviación estándar de cada muestra es una estimación de la desviación estándar de cada población. Minitab utiliza la desviación estándar para estimar la relación en las desviaciones estándar de las poblaciones. Usted debe concentrarse en esta relación.
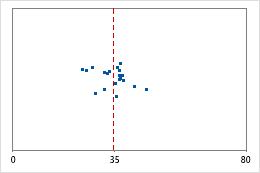
Hospital 1
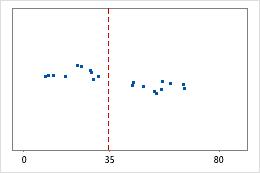
Hospital 2
Tiempos de egreso de un hospital
Los administradores dan seguimiento al tiempo de egreso de los pacientes que son tratados en las áreas de urgencia de dos hospitales. Aunque los tiempos de egreso promedio son aproximadamente iguales (35 minutos), las desviaciones estándar son significativamente diferentes. La desviación estándar del hospital 1 es de aproximadamente 6. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 6 minutos. La desviación estándar del hospital 2 es de aproximadamente 20. En promedio, el tiempo para dar de alta a un paciente se desvía de la media (línea discontinua) aproximadamente 20 minutos.
Varianza
La varianza mide qué tan dispersos están los datos alrededor de su media. La varianza es igual a la desviación estándar elevada al cuadrado.
Interpretación
La varianza de cada muestra es una estimación de la varianza de cada población. Minitab utiliza las varianzas para estimar la relación en las varianzas de las poblaciones. Usted debe concentrarse en esta relación.
Relación estimada de desviaciones estándar
La relación de las desviaciones estándar es la desviación estándar de la primera muestra dividida entre la desviación estándar de la segunda muestra.
Interpretación
La relación estimada de las desviaciones estándar de los datos de la muestra es una estimación de la relación en las desviaciones estándar de las poblaciones.
Puesto que la relación estimada se basa en los datos de una muestra y no en toda la población, es improbable que la relación de las muestras sea igual a la relación de las poblaciones. Para estimar mejor la relación, utilice el intervalo de confianza.
Relación de varianzas estimada
La relación de las varianzas es la varianza de la primera muestra dividida entre la varianza de la segunda muestra.
Interpretación
La relación estimada de las varianzas de los datos de la muestra es una estimación de la relación en las varianzas de las poblaciones.
Puesto que la relación estimada se basa en los datos de una muestra y no en toda la población, es improbable que la relación de las muestras sea igual a la relación de las poblaciones. Para estimar mejor la relación, utilice el intervalo de confianza.
Intervalo de confianza (IC) y límites
El intervalo de confianza proporciona un rango de valores probables para la relación de población. Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces la muestra, un determinado porcentaje de los intervalos o bordes de confianza resultantes contendría la relación de población desconocida. El porcentaje de estos intervalos o bordes de confianza que contiene la relación es el nivel de confianza del intervalo. Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan la relación de población.
Un borde superior define un valor en comparación con el cual es probable que la relación de población sea menor. Un borde inferior define un valor en comparación con el cual es probable que la relación de población sea mayor.
El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra. Para obtener más información, vaya a Maneras de obtener un intervalo de confianza más preciso.
Por opción predeterminada, la prueba de 2 varianzas muestra los resultados del método de Levene y del método de Bonett. El método de Bonett es por lo general más fiable que el método de Levene. Sin embargo, para distribuciones con asimetría extrema y colas pesadas, el método de Levene suele ser más fiable que el método de Bonett. Utilice la prueba F solo si usted está seguro de que los datos siguen una distribución normal. Cualquier desviación pequeña con respecto a la normalidad puede afectar considerablemente los resultados de la prueba F. Para obtener más información, vaya a ¿Debería usar el método de Bonett o el método de Levene para 2 varianzas?.
Relación de desviaciones estándar
| Relación estimada | IC de 95% para la relación usando Bonett | IC de 95% para la relación usando Levene |
|---|---|---|
| 0.658241 | (0.372, 1.215) | (0.378, 1.296) |
En estos resultados, la estimación de la relación de las desviaciones estándar de las poblaciones para las calificaciones de dos hospitales es 0,658. Al utilizar el método de Bonett, usted puede estar 95% seguro de que la relación de las desviaciones estándar de las poblaciones para las calificaciones de los hospitales está entre 0,372 y 1,215.
GL
Los grados de libertad (GL) son la cantidad de información suministrada por sus datos que usted puede "gastar" para estimar los valores de parámetros de población desconocidos y calcular la variabilidad de esas estimaciones. Para una prueba de 2 varianzas, los grados de libertad se determinan según el número de observaciones en la muestra y también dependen del método que Minitab utiliza.
Interpretación
Minitab utiliza los grados de libertad para determinar el estadístico de prueba. Los grados de libertad se determinan según el tamaño de la muestra. Si incrementa el tamaño de la muestra, obtendrá más información sobre la población, con lo cual aumentan los grados de libertad.
Estadístico de prueba para el método de Bonett
El estadístico de prueba es un estadístico que Minitab calcula para el método de Bonett invirtiendo el intervalo de confianza. El estadístico de prueba para el método de Bonett no está disponible para datos resumidos ni para datos que no estén balanceados.
Interpretación
Usted puede comparar el estadístico de prueba con valores críticos de la distribución de chi-cuadrada para determinar si puede rechazar la hipótesis nula. Sin embargo, por lo general es más práctico y conveniente utilizar el valor p de la prueba para hacer la misma determinación. El valor p tiene el mismo significado para pruebas de cualquier tamaño, pero el mismo estadístico de chi-cuadrada puede indicar conclusiones opuestas dependiendo del tamaño de la muestra.
- Para una prueba bilateral, los valores críticos son
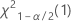y 
. Si el estadístico de prueba es menor que el primer valor o mayor que el segundo valor, usted rechaza la hipótesis nula. Si el estadístico de prueba está entre los valores primero y segundo, no puede rechazar la hipótesis nula. - Para una prueba unilateral con una hipótesis alternativa del tipo "menor que", el valor crítico es
. Si el estadístico de prueba es menor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula. - Para una prueba unilateral del tipo "mayor que", el valor crítico es
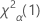. Si el estadístico de prueba es mayor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula.
El estadístico de prueba se utiliza para calcular el valor p.
Estadístico de prueba para el método de Levene
La prueba utiliza el estadístico F de ANOVA de un solo factor aplicado a la desviación de la mediana absoluta de las observaciones. Por lo tanto, aplicar el método de Levene es equivalente a aplicar el procedimiento de ANOVA de un solo factor a la desviación de la mediana absoluta de las observaciones. Para problemas de 2 muestras, este método también es equivalente a aplicar el procedimiento t de 2 muestras a la desviación de la mediana absoluta de las observaciones.
Interpretación
Usted puede comparar el estadístico de prueba con valores críticos de la distribución F para determinar si puede rechazar la hipótesis nula. Sin embargo, por lo general es más práctico y conveniente utilizar el valor p de la prueba para hacer la misma determinación.
- Para una prueba bilateral, los valores críticos son
y 
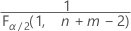. Si el estadístico de prueba es menor que el primer valor o mayor que el segundo valor, usted rechaza la hipótesis nula. Si el estadístico de prueba está entre los valores primero y segundo, no puede rechazar la hipótesis nula. - Para una prueba unilateral con una hipótesis alternativa del tipo "menor que", el valor crítico es
. Si el estadístico de prueba es menor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula. - Para una prueba unilateral del tipo "mayor que", el valor crítico es
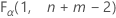. Si el estadístico de prueba es mayor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula.
El estadístico de prueba se utiliza para calcular el valor p.
Estadístico de prueba para el método F
El estadístico de prueba es un estadístico para las pruebas F que mide la relación entre las varianzas observadas.
Interpretación
Usted puede comparar el estadístico de prueba con valores críticos de la distribución F para determinar si puede rechazar la hipótesis nula. Sin embargo, por lo general es más práctico y conveniente utilizar el valor p de la prueba para hacer la misma determinación.
- Para una prueba bilateral, los valores críticos son
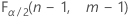y 
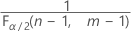. Si el estadístico de prueba es menor que el primer valor o mayor que el segundo valor, usted rechaza la hipótesis nula. Si el estadístico de prueba está entre los valores primero y segundo, no puede rechazar la hipótesis nula. - Para una prueba unilateral con una hipótesis alternativa del tipo "menor que", el valor crítico es
. Si el estadístico de prueba es menor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula. - Para una prueba unilateral del tipo "mayor que", el valor crítico es
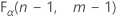. Si el estadístico de prueba es mayor que el valor crítico, usted rechaza la hipótesis nula. De lo contrario, no puede rechazar la hipótesis nula.
El estadístico de prueba se utiliza para calcular el valor p.
Valor p
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Un valor p más pequeño proporciona una evidencia más fuerte en contra de la hipótesis nula.
Interpretación
Utilice el valor p para determinar si la diferencia en las desviaciones estándar o varianzas de las poblaciones es estadísticamente significativa.
- Valor p ≤ α: La relación de las desviaciones estándar o las varianzas es estadísticamente significativa (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, la decisión es rechazar la hipótesis nula. Usted puede concluir que la relación de las desviaciones estándar o las varianzas de las poblaciones no es igual a la relación hipotética. Si no especificó una relación hipotética, Minitab prueba si no existe diferencia entre las desviaciones estándar o las varianzas (Relación hipotética = 1). Utilice su conocimiento especializado para determinar si la diferencia es significativa desde el punto de vista práctico. Para obtener más información, vaya a Significancia estadística y práctica.
- Valor p > α: La relación de las desviaciones estándar o las varianzas no es estadísticamente significativa. (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, la decisión es que no se puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que la relación de las desviaciones estándar o las varianzas de las poblaciones es estadísticamente significativa. Debe asegurarse de que su prueba tenga suficiente potencia para detectar una diferencia que es significativa desde el punto de vista práctico. Para obtener más información, vaya a Potencia y tamaño de la muestra para 2 varianzas.
- La prueba de Bonett es exacta para cualquier distribución continua y no requiere que los datos sean normales. La prueba de Bonett es por lo general más fiable que la prueba de Levene.
- La prueba de Levene también es exacta con cualquier distribución continua. Para distribuciones con asimetría extrema y colas pesadas, el método de Levene tiende a ser más fiable que el método de Bonett.
- La prueba F es exacta solo para datos distribuidos normalmente. Cualquier pequeña desviación con respecto a la normalidad puede causar que la prueba F sea inexacta, incluso con muestras grandes. Sin embargo, si los datos siguen adecuadamente la distribución normal, entonces la prueba F suele ser más poderosa que la prueba de Bonett o la prueba de Levene.
Para obtener más información, vaya a ¿Debería usar el método de Bonett o el método de Levene para 2 varianzas?.
Gráfica de resumen
La gráfica de resumen muestra intervalos de confianza de la relación e intervalos de confianza de las desviaciones estándar o varianzas de cada muestra. La gráfica de resumen también muestra gráficas de caja de los datos de la muestra y los valores p de las pruebas de hipótesis.
Intervalos de confianza
El intervalo de confianza proporciona un rango de valores probables para la relación de población. Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si usted repitiera muchas veces la muestra, un determinado porcentaje de los intervalos o bordes de confianza resultantes contendría la relación de población desconocida. El porcentaje de estos intervalos o bordes de confianza que contiene la relación es el nivel de confianza del intervalo. Por ejemplo, un nivel de confianza de 95% indica que si usted toma 100 muestras aleatorias de la población, podría esperar que aproximadamente 95 de las muestras produzcan intervalos que contengan la relación de población.
Un borde superior define un valor en comparación con el cual es probable que la relación de población sea menor. Un borde inferior define un valor en comparación con el cual es probable que la relación de población sea mayor.
Interpretación
El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra. Para obtener más información, vaya a Maneras de obtener un intervalo de confianza más preciso.
Por opción predeterminada, la prueba de 2 varianzas muestra los resultados del método de Levene y del método de Bonett. El método de Bonett es por lo general más fiable que el método de Levene. Sin embargo, para distribuciones con asimetría extrema y colas pesadas, el método de Levene suele ser más fiable que el método de Bonett. Utilice la prueba F solo si usted está seguro de que los datos siguen una distribución normal. Cualquier desviación pequeña con respecto a la normalidad puede afectar considerablemente los resultados de la prueba F. Para obtener más información, vaya a ¿Debería usar el método de Bonett o el método de Levene para 2 varianzas?.
Gráfica de caja
Una gráfica de caja proporciona un resumen gráfico de la distribución de cada muestra. La gráfica de caja permite comparar fácilmente la forma, tendencia central y variabilidad de las muestras.
Interpretación
Utilice una gráfica de caja para examinar la dispersión de los datos y para identificar cualquier posible valor atípico. Las gráficas de caja funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
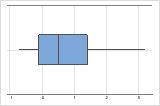
Asimétrico hacia la derecha
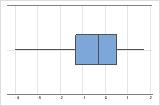
Asimétrico hacia la izquierda
La gráfica de caja con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. La gráfica de caja con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Los datos marcadamente asimétricos pueden afectar la validez del valor p si la muestra es pequeña (cualquiera de las muestras tiene menos de 20 valores). Si los datos son marcadamente asimétricos y usted tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
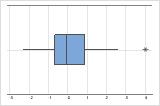
En una gráfica de caja, los asteriscos (*) denotan valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
Gráfica de valores individuales
Una gráfica de valores individuales muestra los valores individuales en cada muestra. Una gráfica de valores individuales permite comparar fácilmente las muestras. Cada círculo representa una observación. Una gráfica de valores individuales es especialmente útil cuando usted tiene relativamente pocas observaciones y cuando también necesita evaluar el efecto de cada observación.
Interpretación
Utilice una gráfica de valores individuales para examinar la dispersión de los datos y para identificar cualquier posible valor atípico. Las gráficas de valores individuales funcionan mejor cuando el tamaño de la muestra es menor que 50.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
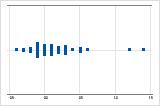
Asimétrico hacia la derecha
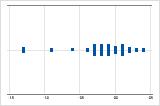
Asimétrico hacia la izquierda
La gráfica de valores individuales con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. La gráfica de valores individuales con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Los datos marcadamente asimétricos pueden afectar la validez del valor p si la muestra es pequeña (cualquiera de las muestras tiene menos de 20 valores). Si los datos son marcadamente asimétricos y usted tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
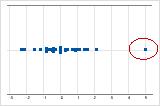
En una gráfica de valores individuales, los valores de datos extrañamente bajos o altos indican posibles valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
Histograma
Un histograma divide los valores de la muestra en muchos intervalos y representa la frecuencia de los valores de datos en cada intervalo con una barra.
Interpretación
Utilice un histograma para evaluar la forma y dispersión de los datos. Los histogramas funcionan mejor cuando el tamaño de la muestra es mayor que 20.
- Datos asimétricos
-
Examine la dispersión de los datos para determinar si los datos parecen ser asimétricos. Cuando los datos son asimétricos, la mayoría de los datos se ubican en la parte superior o inferior de la gráfica. Con frecuencia, es fácil detectar la asimetría con un histograma o una gráfica de caja.
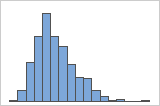
Asimétrico hacia la derecha
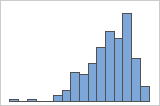
Asimétrico hacia la izquierda
El histograma con datos asimétricos hacia la derecha muestra tiempos de espera. La mayoría de los tiempos de espera son relativamente cortos y solo unos pocos son largos. El histograma con datos asimétricos hacia la izquierda muestra datos de tiempo de falla. Unos pocos elementos fallan inmediatamente y muchos otros fallan posteriormente.
Los datos marcadamente asimétricos pueden afectar la validez del valor p si la muestra es pequeña (cualquiera de las muestras tiene menos de 20 valores). Si los datos son marcadamente asimétricos y usted tiene una muestra pequeña, considere aumentar el tamaño de la muestra.
- Valores atípicos
-
Los valores atípicos, que son valores de datos que están muy distantes de otros valores de datos, pueden afectar considerablemente los resultados de un análisis. Con frecuencia, es fácil identificar los valores atípicos en una gráfica de caja.
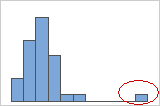
En un histograma, las barras aisladas en cualquiera de los extremos de la gráfica identifican posibles valores atípicos.
Trate de identificar la causa de cualquier valor atípico. Corrija cualquier error de entrada de datos o de medición. Considere eliminar los valores de datos asociados con eventos anormales y únicos (también conocidos como causas especiales). Luego, repita el análisis. Para obtener más información, vaya a Identificar valores atípicos.
